已知函数 满足对任意实数
满足对任意实数 都有
都有 成立,且当
成立,且当 时,
时, ,
, .
.
(1)求 的值;
的值;
(2)判断 在
在 上的单调性,并证明;
上的单调性,并证明;
(3)若对于任意给定的正实数 ,总能找到一个正实数
,总能找到一个正实数 ,使得当
,使得当 时,
时, ,则称函数
,则称函数 在
在 处连续。
处连续。
试证明: 在
在 处连续.
处连续.
(本小题满分12分)已知等差数列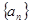 满足:
满足: ,
, ,该数列的前三项分别加上
,该数列的前三项分别加上 后顺次成为等比数列
后顺次成为等比数列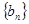 的前三项
的前三项
(1)分别求数列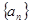 ,
,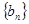 的通项公式
的通项公式 ,
, ;
;
(2)设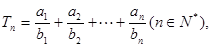 若
若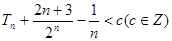 恒成立,求
恒成立,求 的最小值.
的最小值.
(本小题满分12分)如图,三角形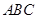 中,
中,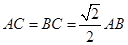 ,
, 是边长为
是边长为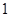 的正方形,平面
的正方形,平面 ⊥平面
⊥平面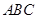 ,若
,若 分别是
分别是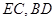 的中点.
的中点.
(1)求证: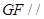 平面
平面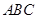 ;
;
(2)求证: ⊥平面
⊥平面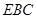 ;
;
(3)求几何体 的体积.
的体积.
(本小题满分12分)甲乙两人用四张扑克牌(红桃2,红桃3,红桃4,方片4)玩游戏,将牌洗匀后,背面朝上,按如下规则抽取:甲先抽,乙后抽,抽取的牌不放回,各抽取一张。
写出甲乙两人抽到牌的所有情况;
若甲抽到红桃3,则乙抽出的牌的牌面数字比3大的概率是多少?
甲乙约定:若甲抽出的牌的牌面数字比乙大,则甲胜;反之,则乙胜.你认为此游戏是否公平?说明你的理由.
(本小题满分12分)在 中,角
中,角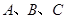 的对边分别为
的对边分别为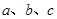 ,
,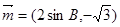 ,
,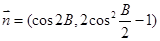 ,且
,且  .
.
(1)求锐角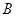 的大小;
的大小;
(2)若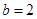 ,求
,求 面积的最大值.
面积的最大值.
已知函数 .
.
(1)当 时,求证:
时,求证: ;
;
(2)当 时,
时, 恒成立,求实数
恒成立,求实数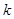 的值.
的值.