为了对某课题进行研究,用分层抽样方法从三所高校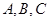 的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
| 高校 |
相关人数 |
抽取人数 |
| A |
18 |
x |
| B |
36 |
2 |
| C |
54 |
y |
(1)求 、
、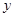 ;
;
(2)若从高校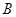 、
、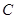 抽取的人中选2人作专题发言,求这2人都来自高校
抽取的人中选2人作专题发言,求这2人都来自高校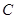 的概率.
的概率.
已知椭圆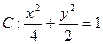 和圆
和圆 ,且圆C与x轴交于A1,A2两点(1)设椭圆C1的右焦点为F,点P的圆C上异于A1,A2的动点,过原点O作直线PF的垂线交椭圆的右准线交于点Q,试判断直线PQ与圆C的位置关系,并给出证明。(2)设点
,且圆C与x轴交于A1,A2两点(1)设椭圆C1的右焦点为F,点P的圆C上异于A1,A2的动点,过原点O作直线PF的垂线交椭圆的右准线交于点Q,试判断直线PQ与圆C的位置关系,并给出证明。(2)设点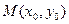 在直线
在直线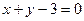 上,若存在点
上,若存在点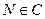 ,使得
,使得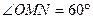 (O为坐标原点),求
(O为坐标原点),求 的取值范围。
的取值范围。
(本小题满分14分)已知函数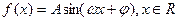 (其中A>0,
(其中A>0, )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为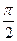 ,且图象上一个最低点为
,且图象上一个最低点为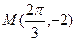 .(Ⅰ)求
.(Ⅰ)求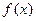 的解析式;(Ⅱ)当
的解析式;(Ⅱ)当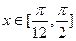 ,求
,求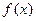 的值域;
的值域;
(本小题满分16分)已知集合M是满足下列性质的函数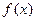 的全体:若存在非零常数k,对任意
的全体:若存在非零常数k,对任意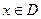 ,等式
,等式 恒成立。(Ⅰ)判断一次函数
恒成立。(Ⅰ)判断一次函数 是否属于集合M;(Ⅱ)证明
是否属于集合M;(Ⅱ)证明 属于集合M,并找到一个常数k;(Ⅲ)已知函数
属于集合M,并找到一个常数k;(Ⅲ)已知函数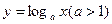 与
与 的图像有公共点,试证明
的图像有公共点,试证明
(本小题满分16分)已知函数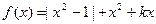 (Ⅰ)若
(Ⅰ)若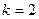 ,求方程
,求方程 的解(Ⅱ)若关于x的方程
的解(Ⅱ)若关于x的方程 在(0,2)上有两个解
在(0,2)上有两个解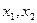 ,求k的取值范围。
,求k的取值范围。
(本小题满分16分)已知数列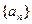 的前n项和为Sn,点
的前n项和为Sn,点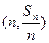 的直线
的直线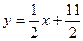 上,数列
上,数列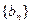 满足
满足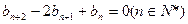 ,
,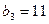 ,且
,且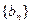 的前9项和为153.
的前9项和为153.
(Ⅰ)求数列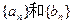 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设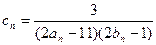 ,记数列
,记数列 的前n项和为Tn,求使不等式
的前n项和为Tn,求使不等式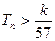 对一切
对一切 都成立的最大正整数k的值.
都成立的最大正整数k的值.