(本小题满分12分)四川灾后重建工程督导评估小组五名专家被随机分配到A、B、C、D四所不同的学校进行重建评估工作,要求每所学校至少有一名专家。
(1)求评估小组中甲、乙两名专家同时被分配到A校的概率;
(2)求评估小组中甲、乙两名专家不在同一所学校的概率;
(3)设随机变量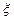 为这五名专家到A校评估的人数,求
为这五名专家到A校评估的人数,求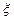 的数学期望E
的数学期望E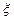 。
。
(本小题满分10分)选修4-5:不等式选 讲
讲
已知函数 .
.
(Ⅰ) =1时,求
=1时,求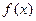 的值域;
的值域;
(Ⅱ)若 的解集是全体实数,求
的解集是全体实数,求 的取值范围.
的取值范围.
(本小题满分10分)
已知曲线 的参数方程为
的参数方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为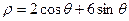 .
.
(Ⅰ)将曲线 的参数方程化为普通方程,将曲线
的参数方程化为普通方程,将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)曲线 ,
, 是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
四、选考题(本题满分10分,请从所给的三道题中任选一题做答,并在答题卡上填写所选题目的题号,如果多做,则按所做的第一题记分.)
(本小题满分10分)选修4-1:几何证明选讲
如图,△ABC的角平分线AD的延长线交它的外接圆于点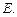
(Ⅰ)证明:△ABE∽△ADC;
(Ⅱ)若△ABC的面积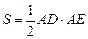 ,求
,求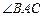 的大小.
的大小.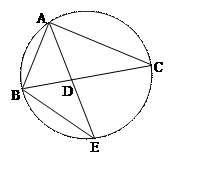
(本小题满分12分)
已知函数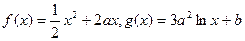 ,
,
(Ⅰ)设两曲线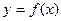 与
与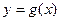 有公共点,且在公共点处的切线相同,若
有公共点,且在公共点处的切线相同,若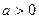 ,试建立
,试建立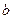 关于
关于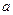 的函数关系式;
的函数关系式;
(Ⅱ)若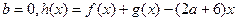 在(0,4)上为单调函数,求
在(0,4)上为单调函数,求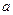 的取值范围.
的取值范围.