已知函数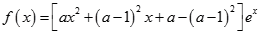 (其中
(其中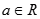 ).
).
(1)若 为
为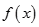 的极值点,求
的极值点,求 的值;
的值;
(2)在(1)的条件下,解不等式 .
.
某村电费收取有以下两种方案供农户选择:
方案一:每户每月收管理费2元,月用电不超过30度时,每度0.5元,超过30度时,超过部分按每度0.6元收取.
方案二:不收管理费,每度0.58元.
(1)求方案一收费 元与用电量
元与用电量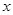 (度)间的函数关系;
(度)间的函数关系;
(2)老王家九月份按方案一交费35元,问老王家该月用电多少度?
(3)老王家月用电量在什么范围时,选择方案一比选择方案二更好?
已知函数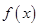 是二次函数,且满足
是二次函数,且满足 ;函数
;函数 .
.
(1)求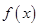 的解析式;
的解析式;
(2)若 ,且
,且 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
设 ,
,
(1)若 ,求
,求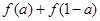 的值;
的值;
(2)求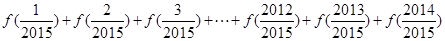 的值.
的值.
若集合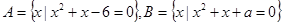 ,且
,且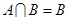 ,求实数
,求实数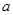 的取值集合.
的取值集合.
证明“0≤a≤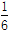 ”是“函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为减函数”的充分不必要条件.
”是“函数f(x)=ax2+2(a-1)x+2在区间(-∞,4]上为减函数”的充分不必要条件.