如图，三棱锥A﹣BCD中，AB⊥底面BCD，BC⊥CD，且AB=BC=1，CD=2，点E为CD的中点，则AE的长为（ ）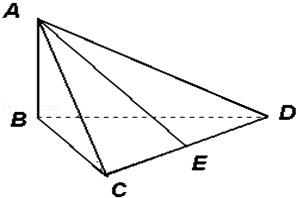
A． |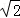
B． |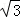
C．2 | D． |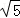
已知圆（x﹣a）2+（y﹣b）2=r2的圆心为抛物线y2=4x的焦点，且与直线3x+4y+2=0相切，则该圆的方程为（）
A． |
B． |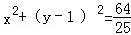
| C．（x﹣1）2+y2=1 |
| D．x2+（y﹣1）2=1 |
过双曲线
的左焦点F（﹣c，0），（c＞0），作圆：x2+y2=
的切线，切点为E，延长FE交双曲线右支于点P，若
=
（
+
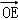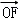），则双曲线的离心率为（）
A． |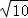
B． |
C． |
D． |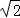
过双曲线
﹣
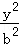=1（a＞0，b＞0）的左焦点F1（﹣c，0）（c＞0）作圆x2+y2=
的切线，切点为E，直线F1E交双曲线右支于点P，若
=
（
+
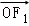），则双曲线的离心率为（）
A． |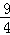
B． |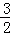
C． |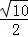
D． |
过双曲线
（a＞0，b＞0）的左焦点F（﹣c，0）作圆x2+y2=a2的切线，切点为E，延长FE交抛物线y2=4cx于点P，若E为线段FP的中点，则双曲线的离心率为（）
A． |
B． |
C．+1 |
D． |
已知圆P：x2+y2=4y及抛物线S：x2=8y，过圆心P作直线l，此直线与上述两曲线的四个交点，自左向右顺次记为A，B，C，D，如果线段AB，BC，CD的长按此顺序构成一个等差数列，则直线l的斜率为（）
A．± |
B． |
C．± |
D． |