如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.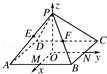
已知直角梯形 ,
, 是
是 边上的中点(如图甲),
边上的中点(如图甲), ,
, ,
,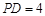 ,将
,将 沿
沿 折到
折到 的位置,使
的位置,使 ,点
,点 在
在 上,且
上,且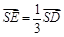 (如图乙)
(如图乙)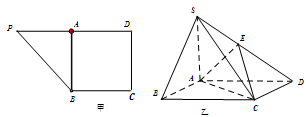
(Ⅰ)求证: 平面ABCD.
平面ABCD.
(Ⅱ)求二面角E−AC−D的余弦值
某旅游公司提供甲、乙、丙三处旅游景点,游客选择游玩哪个景点互不影响,已知某游客选择游甲地而不选择游乙地和丙地的概率为0.08,选择游甲地和乙地而不选择游丙地的概率为0.12,在甲、乙、丙三处旅游景点中至少选择游一个景点0.88,用 表示游客在甲、乙、丙三处旅游景点中选择游玩的景点数和没有选择游玩的景点数的乘积.
表示游客在甲、乙、丙三处旅游景点中选择游玩的景点数和没有选择游玩的景点数的乘积.
(Ⅰ)记“函数 是R上的偶函数”为事件A,求事件A的概率;
是R上的偶函数”为事件A,求事件A的概率;
(Ⅱ)求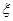 的概率分布列及数学期望.
的概率分布列及数学期望.
已知函数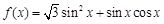 .
.
(Ⅰ)求函数 在区间
在区间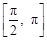 上的零点;
上的零点;
(Ⅱ)设 ,求函数
,求函数 的图象的对称轴方程
的图象的对称轴方程
在平面直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为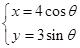 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系,得曲线
轴的非负半轴为极轴建立极坐标系,得曲线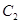 的极坐标方程为
的极坐标方程为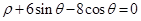 (
( )
)
(Ⅰ)求曲线 的普通方程和曲线
的普通方程和曲线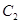 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线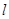 :
: 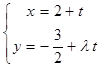 (
( 为参数)过曲线
为参数)过曲线 与
与 轴负半轴的交点,求与直线
轴负半轴的交点,求与直线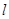 平行且与曲线
平行且与曲线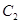 相切的直线方程
相切的直线方程
设 (
( 且
且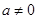 )
)
(Ⅰ)讨论函数 的单调性;
的单调性;
(Ⅱ)若 ,证明:
,证明: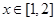 时,
时, 成立
成立