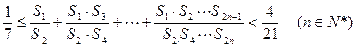已知函数y=xlnx
（1）求这个函数的导数；
（2）求这个函数的图象在点x=1处的切线方程．
（本小题满分12分）在一次食品卫生大检查中，执法人员从抽样中得知，目前投放我市的甲、乙两种食品的合格率分别为
和
．
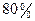（1）今有三位同学聚会,若每人分别从两种食品中任意各取一件,求恰好有一人取到两件都是不合格品的概率．
（2）若某消费者从两种食品中任意各购一件,设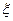
表示购得不合格食品的件数,试写出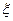
的分布列,并求其数学期望．
四边形ABCD中， BD是它的一条对角线，且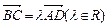
，
，
．
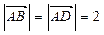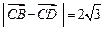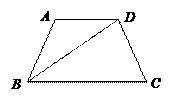
⑴若△BCD是直角三形，求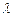
的值；
⑵在⑴的条件下，求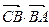
．
（本大题12分，）如图，三棱柱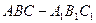
的底面是边长为2的正三角形且侧棱垂直于底面，侧棱长是，D是AC的中点。
（1）求证：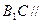
平面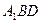
；
（2）求二面角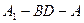
的大小；
（3）求直线
与平面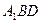所成的角的正弦值．
（本小题满分12分）设函数
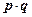,其中
,
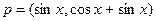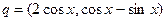,x∈R.
（I）求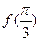
的值及函数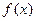
的最大值；
（II）求函数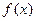的单调递增区间.
（本小题满分12分） 古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏，其玩法如下：如图，设有n（
）个圆盘依其半径大小，大的在下，小的在上套在A柱上，现要将套在A柱上的盘换到C柱上，要求每次只能搬动一个，而且任何时候不允许将大盘套在小盘上面，假定有三根柱子A、B、C可供使用．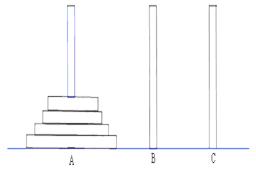
现用an表示将n个圆盘全部从A柱上移到C柱上所至少需要移动的次数，回答下列问题：
(1)写出a1，a2，a3，并求出an；
(2)记
，求和
（
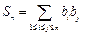）；（其中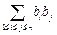
表示所有的积
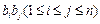的和）
(3)证明：