袋中有分别写着“团团”和“圆圆”的两种玩具共 个且形状完全相同,从中任取
个且形状完全相同,从中任取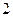 个玩具都是“圆圆”的概率为
个玩具都是“圆圆”的概率为 ,
, 、
、 两人不放回从袋中轮流摸取一个玩具,
两人不放回从袋中轮流摸取一个玩具, 先取,
先取, 后取,然后
后取,然后 再取,……
再取,…… 直到两人中有一人取到“圆圆”时即停止游戏.每个玩具在每一次被取出的机会是均等的,用
直到两人中有一人取到“圆圆”时即停止游戏.每个玩具在每一次被取出的机会是均等的,用 表示游戏终止时取玩具的次数.
表示游戏终止时取玩具的次数.
(1)求 时的概率;
时的概率;
(2)求 的数学期望.
的数学期望.
(本小题满分10分)已知圆 :
: 关于直线
关于直线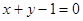 对称,圆心
对称,圆心 在第四象限,半径为
在第四象限,半径为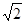 .
.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)是否存在直线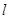 与圆
与圆 相切,且在
相切,且在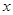 轴上的截距是y轴上的截距的
轴上的截距是y轴上的截距的 倍?若存在,求直线
倍?若存在,求直线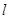 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(本小题满分10分)
如图,平面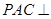 平面
平面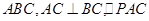 为等边三角形,
为等边三角形, 分别是线段
分别是线段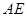 ,
, 上的动点,且满足:
上的动点,且满足: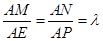
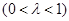 .
.
(Ⅰ)求证: ∥平面
∥平面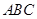 ;
;
(Ⅱ)当 时,求平面ABC与平面MNC所成的锐二面角的大小.
时,求平面ABC与平面MNC所成的锐二面角的大小.
(本小题满分10分)如图,在四棱锥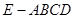 中,底面
中,底面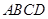 为正方形,
为正方形, 平面
平面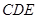 ,已知
,已知 .
.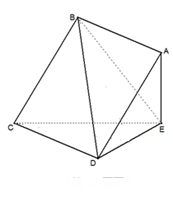
(Ⅰ)求证:平面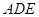
 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
如图,直线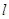 过点
过点 ,夹在两已知直线
,夹在两已知直线 和
和 之间的线段
之间的线段 恰被点
恰被点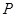 平分.
平分.
(Ⅰ)求直线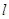 的方程;
的方程;
(Ⅱ)设点 ,且
,且 ,求:
,求: 的面积.
的面积.
已知 ,
,
(1)若f(x)的最小值记为h(a),求h(a)的解析式.
(2)是否存在实数m,n同时满足以下条件:① ;②当h(a)的定义域为[n,m]时,值域为[n2,m2];若存在,求出m,n的值;若不存在,说明理由.
;②当h(a)的定义域为[n,m]时,值域为[n2,m2];若存在,求出m,n的值;若不存在,说明理由.