(本小题满分12分)
已知函数 的图象与
的图象与 轴的交点为
轴的交点为 ,它在
,它在 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为 和
和 .
.
(1)求 的解析式;
的解析式;
(2)若锐角 满足
满足 ,求
,求 的值.
的值.
某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间。按年龄分组:第1组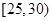 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组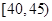 ,第5组
,第5组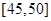 ,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,在其右面的表是年龄的频率分布表。
(1)求正整数a,b,N的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组中抽取的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1 人在第3组的概率。
(1)已知函数 , 编写程序求函数值(只写程序)
, 编写程序求函数值(只写程序)
(2)画出程序框图:求和: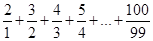 (只画程序框图,循环体不对不得分)
(只画程序框图,循环体不对不得分)
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x |
6 |
8 |
10 |
12 |
| y |
2 |
3 |
5 |
6 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
(2)试根据已求出的线性回归方程,预测记忆力为9的同学的判断力.
已知曲线C:
(1)当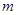 为何值时,曲线C表示圆;
为何值时,曲线C表示圆;
(2)在(1)的条件下,若曲线C与直线 交于M、N两点,且
交于M、N两点,且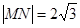 ,求
,求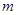 的值.
的值.
(3)在(1)的条件下,设直线 与圆
与圆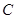 交于
交于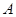 ,
, 两点,是否存在实数
两点,是否存在实数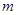 ,使得以
,使得以 为直径的圆过原点,若存在,求出实数
为直径的圆过原点,若存在,求出实数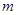 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形. 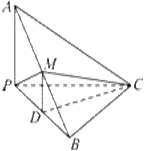
(1)求证DM∥平面APC;
(2)求证平面ABC⊥平面APC;
(3)若BC=PC=4,求二面角P-AB-C的正弦值.