如图, 为抛物线
为抛物线 的焦点,
的焦点, 为抛物线内一定点,
为抛物线内一定点, 为抛物线上一动点,且
为抛物线上一动点,且 的最小值为
的最小值为 .
.

(1)求该抛物线的方程;
(2)如果过 的直线
的直线 交抛物线于
交抛物线于 、
、 两点,且
两点,且 ,求直线
,求直线 的倾斜角的取值范围.
的倾斜角的取值范围.
(本小题满分12分)
己知函数 
(1)若关于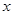 的不等式
的不等式 恒成立,求整数
恒成立,求整数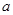 的最小值;
的最小值;
(2)若 ,正实数
,正实数 满足
满足 ,证明:
,证明: 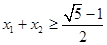
(本小题满分12分)
已知椭圆C: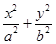 =1(
=1(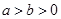 )的离心率与双曲线
)的离心率与双曲线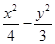 =1的一条渐近线的斜率相等,以原点为圆心,椭圆的短半轴长为半径的圆与直线
=1的一条渐近线的斜率相等,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切(
相切(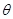 为常数).
为常数).
(1)求椭圆C的方程;
(2)若过点 的直线与椭圆
的直线与椭圆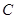 相交
相交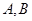 两点,设
两点,设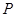 为椭圆上一点,且满足
为椭圆上一点,且满足 (
( 为坐标原点),当
为坐标原点),当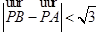 时,求实数
时,求实数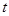 取值范围.
取值范围.
(本小题满分12分)
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,
∠BAD=∠CDA=90°,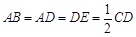 ,M是线段AE上的动点.
,M是线段AE上的动点.
(1)试确定点M的位置,使AC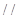 平面DMF,并说明理由;
平面DMF,并说明理由;
(2)在(1)的条件下,求平面DMF与平面ABCD所成锐二面角的余弦值.
(本小题满分12分)
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取 个作为样本,称出它们的重量(单位:克),重量分组区间为
个作为样本,称出它们的重量(单位:克),重量分组区间为 ,
, ,
, ,
, ,由此得到样本的重量频率分布直方图(如下图),
,由此得到样本的重量频率分布直方图(如下图),
(1)求 的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
(2)从盒子中随机抽取 个小球,其中重量在
个小球,其中重量在 内的小球个数为
内的小球个数为 ,求
,求 的分布列和数学期望. (以直方图中的频率作为概率).
的分布列和数学期望. (以直方图中的频率作为概率).
(本小题满分12分)
已知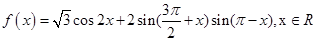
(1)求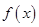 最小正周期及单调增区间;
最小正周期及单调增区间;
(2)已知锐角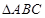 的内角
的内角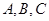 的对边分别为
的对边分别为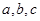 ,且
,且 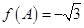 ,
,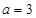 ,
,
求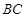 边上的高的最大值.
边上的高的最大值.