已知圆
，定点N（1，0），
是圆
上任意一点，线段
的垂直平分线
交
于点
，点的轨迹为曲线
。
（Ⅰ）求曲线的方程；
（2）若直线
与曲线相交于
，
两点（
不是左右顶点），且以
为直径的圆过椭圆的右顶点，求证：直线过定点，并求出该定点的坐标．
（本小题满分12分）解下列不等式:
(1)-x2+2x-
>0; 
(2)9x2-6x+1≥0.
（本小题满分12分）已知数列{an}满足 a1＝1,an＋1＝
.,写出它的前5项,并归纳出数列的一个通项公式
(不要求证明)
已知椭圆的焦点在
轴上，短轴长为4，离心率为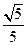
.
(1)求椭圆的标准方程；
(2)若直线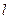
过该椭圆的左焦点，交椭圆于M、N两点，且
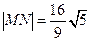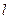，求直线的方程.
已知等差数列{an}的前n项的和记为Sn．如果a4＝－12，a8＝－4．
(1)求数列{an}的通项公式；
(2)求Sn的最小值及其相应的n的值；
(3)从数列{an}中依次取出a1，a2，a4，a8，…，
，…，构成一个新的数列{bn}，求{bn}的前n项和．
命题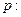
方程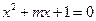
有两个不等的正实数根，命题
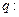方程
无实数根。若“
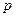或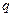
”为真命题，求
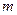的取值范围。