如图△ABC中，点O是AC上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠GCA的平分线于点F．
（1）说明 EO=FO．
（2）当点O运动到何处，四边形AECF是矩形？说明你的结论．
（3）当点O运动到何处，AC与BC具有怎样的关系时，四边形AECF是正方形？为什么？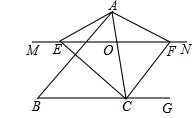
如图已知点C为AB上一点，AC=12cm，CB=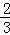
AC，D、E分别为AC、AB的中点，求DE的长．
解方程
（1）3x﹣7（x﹣1）=3﹣2（x+3）
（2）x﹣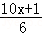
=
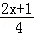﹣1．
尺规作图（不写作法，仅保留作图痕迹，在原图上不给分）：
已知线段a、b（a＜b），求作线段AB，使AB=b﹣a．
如图，平面上有四个点A、B、C、D，根据下列语句画图．
（1）画直线AB；作射线BC；画线段CD；
（2）连接AD，并将其反向延长至E，使DE=2AD；
（3）找到一点F，使点F到A、B、C、D四点距离和最短．
如图：抛物线y=－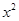
+bx+c与x轴交于A、B两点，与y轴交于点C，且∠BAC=α，∠ABC=
，tanα－tanβ=2，∠ACB=90°．
（1）求点C的坐标；
（2）求抛物线的解析式；
（3）若抛物线的顶点为P，求四边形ABPC的面积．