点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.利用数形结合思想回答下列问题:
(1)数轴上表示1和5两点之间的距离是 ,数轴上表示2和-1的两点之间的距离是 ;
(2)数轴上表示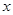 和-1的两点之间的距离表示为 ;
和-1的两点之间的距离表示为 ;
(3)若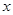 表示一个有理数,且
表示一个有理数,且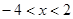 ,则
,则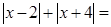 ;
;
(4)利用数轴求出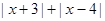 的最小值,并写出此时
的最小值,并写出此时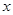 可取哪些整数值?(4 分)
可取哪些整数值?(4 分)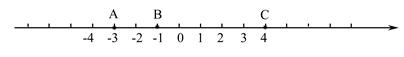
某蔬菜加工厂承担出口蔬菜加工任务,有一批蔬菜产品需要装入某一规格的纸箱.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为4元;
方案二:由蔬菜加工厂租赁机器自己加工制作这种纸箱,机器租赁费按生产纸箱数收取.工厂需要一次性投入机器安装等费用16000元,每加工一个纸箱还需成本费2.4元.
(1)若需要这种规格的纸箱 个,请分别写出从纸箱厂购买纸箱的费用
个,请分别写出从纸箱厂购买纸箱的费用 (元)和蔬菜加工厂自己加工制作纸箱的费用
(元)和蔬菜加工厂自己加工制作纸箱的费用 (元)关于
(元)关于 (个)的函数关系式;
(个)的函数关系式;
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
已知:抛物线 的对称轴为
的对称轴为 与
与 轴交于
轴交于 两点,与
两点,与 轴交于点
轴交于点 其中
其中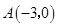 、
、

(1)求这条抛物线的函数表达式.
(2)已知在对称轴上存在一点P,使得 的周长最小.请求出点P的坐标.
的周长最小.请求出点P的坐标.
某中学九年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.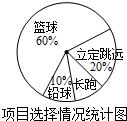

请你根据图表中的信息回答下列问题:
(1)求选择长跑训练的人数占全班人数的百分比及该班
学生的总人数;
(2)求训练后篮球定时定点投篮人均进球数;
(3)根据测试资料,训练后篮球定时定点投篮的人均进球数比训练之前人均进球数
增加25%。请求出参加训练之前的人均进球数。
(1)解方程:
(2)当 为何值时,关于
为何值时,关于 的方程
的方程 有两个实数根.
有两个实数根.
(1)计算: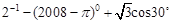
(2) 子求值。
子求值。