已知函数 =
= .
.
(1)求函数 的单调区间;
的单调区间;
(2)若函数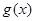 =
= 在[-2,
在[-2, ]恰有2解,求实数
]恰有2解,求实数 的取值范围.
的取值范围.
已知圆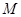 :
: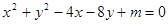 与
与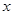 轴相切,点
轴相切,点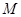 为圆心.
为圆心.
(1)求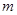 的值;
的值;
(2)求圆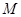 在
在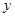 轴上截得的弦长;
轴上截得的弦长;
(3)若点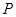 是直线
是直线 上的动点,过点
上的动点,过点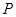 作直线
作直线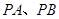 与圆
与圆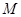 相切,
相切,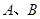 为切点.求四边形
为切点.求四边形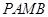 面积的最小值。
面积的最小值。
已知角 的终边过点
的终边过点 .
.
(1)求 的值;
的值;
(2)若 为第三象限角,且
为第三象限角,且 ,求
,求 的值.
的值.
某学校高一年学生在某次数学单元测试中,成绩在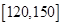 的频数分布表如下:
的频数分布表如下:
| 分数 |
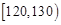 |
 |
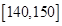 |
| 频数 |
60 |
20 |
20 |
(1)用分层抽样的方法从成绩在 ,
, 和
和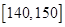 的同学中共抽取
的同学中共抽取 人,其中成绩在
人,其中成绩在 的有几人?
的有几人?
(2)从(1)中抽出的 人中,任取
人中,任取 人,求成绩在
人,求成绩在 和
和 中各有
中各有 人的概率?
人的概率?
已知数列{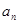 }是等差数列,其中每一项及公差
}是等差数列,其中每一项及公差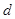 均不为零,设
均不为零,设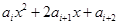 =0(
=0( )是关于
)是关于 的一组方程.
的一组方程.
(1)求所有这些方程的公共根;
(2)设这些方程的另一个根为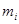 ,求证
,求证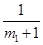 ,
,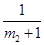 ,
, ,…,
,…, 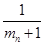 ,…也成等差数列.
,…也成等差数列.
老峰镇计划建造一个室内面积为800 的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3  宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?
宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?