已知,如图,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l: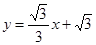 对称.
对称.
(1)求A、B两点坐标,并证明点A在直线l上;
(2)求二次函数解析式;
(3)过点B作直线BK∥AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN+NM+MK和的最小值.
徒骇河风景区建设是今年我市重点工程之一,某工程公司承担了一段河底清淤任务,需清淤4万方,清淤1万方后,该公司为提高施工进度,又新增一批工程机械参与施工,工效提高到原来的2倍,共用25天完成任务,问该工程公司新增工程机械后每天清淤多少方?
某品牌瓶装饮料每箱价格26元,某商店对该瓶装饮料进行“买一送三”促销活动,若整箱购买,则买一箱送三瓶,这相当于每瓶比原价便宜了0.6元.问该品牌饮料一箱有多少瓶?
(2011山东济宁,21,8分)某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.
(1)甲、乙工程队每天各能铺设多少米?
(2)如果要求完成该项工程的工期不超过10天,那么为两工程队分配工程量(以百米为单位)的方案有几种?请你帮助设计出来.
某品牌瓶装饮料每箱价格26元,某商店对该瓶装饮料进行“买一送三”促销活动,若整箱购买,则买一箱送三瓶,这相当于每瓶比原价便宜了0.6元.问该品牌饮料一箱有多少瓶?
解分式方程: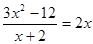 .
.