对于函数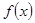
，若存在
，使
成立，则称
为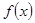的不动点.已知函数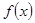
.
（1）当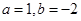
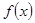时，求的不动点；
（2）若对于任意实数
，函数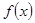恒有两个相异的不动点，求
的取值范围.
如图，已知C点在圆O直径BE的延长线上，CA切圆O于A点，DC是∠ACB的平分线交AE于点F，交AB于D点．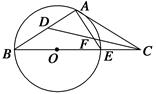
(1)求∠ADF的度数；
(2)AB＝AC，求AC∶BC.
如图所示，圆内的两条弦AB、CD相交于圆内一点P，已知PA＝PB＝4，PC＝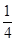
PD.求CD的长．
如图所示，已知AB是⊙O的直径，C为圆上任意一点，过C的切线分别与过A、B两点的切线交于P、Q.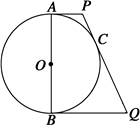
求证：AB2＝4AP·BQ.
如图所示，在△ABC中，I为△ABC的内心，AI交BC于D，交△ABC外接圆于E.
求证：(1)IE＝EC；
(2)IE2＝ED·EA.
如图，已知C点在圆O直径BE的延长线上，CA切圆O于A点，DC是∠ACB的平分线交AE于点F，交AB于D点．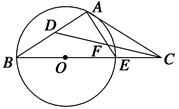
(1)求∠ADF的度数；
(2)AB＝AC，求AC∶BC.