本小题满分13分)
如图,已知ABCD是边长为2的正方形,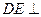 平面ABCD,
平面ABCD, 平面ABCD,且FB=2DE=2。
平面ABCD,且FB=2DE=2。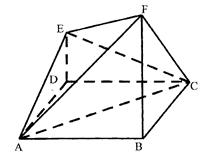
(1)求点E到平面FBC的距离;
(2)求证:平面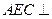 平面AFC。
平面AFC。
(本小题满分13分)
某射手A第n次射击时击中靶心的概率为
(1)求A射击5次,直到第5次才击中靶心的概率P;
(2)若A共射击3次,求恰好击中1次靶心的概率。
(本小题满分13分)
在 中,边a,b,c分别为角A,B,C的对边,若
中,边a,b,c分别为角A,B,C的对边,若 ,且
,且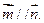
(1)求角A的大小;
(2)若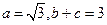 ,求
,求 的面积S。
的面积S。
(本小题满分8分)如图,直三棱柱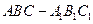 中,
中,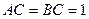 ,
,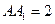 ,
,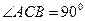 , M是A1B1的中点
, M是A1B1的中点
(1)求证C1M^平面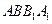 ;
;
(2)求异面直线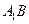 与
与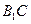 所成角的余弦值
所成角的余弦值
已知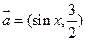 ,
,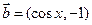 .
.
(1)若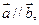 求
求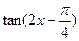 的值;(2)设
的值;(2)设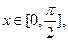 求
求 的最小值。
的最小值。