本小题满分13分)
如图,已知ABCD是边长为2的正方形,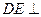 平面ABCD,
平面ABCD, 平面ABCD,且FB=2DE=2。
平面ABCD,且FB=2DE=2。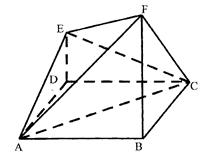
(1)求点E到平面FBC的距离;
(2)求证:平面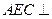 平面AFC。
平面AFC。
(本小题满分12分)设为 的内角
的内角 、
、 、
、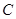 所对的边分别为
所对的边分别为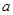 、
、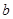 、
、 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若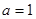 ,求
,求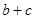 的最值.
的最值.
(本小题满分14分)
(1)当 时,求
时,求 的极值点.
的极值点.
(2)若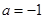 ,
, 的图象与
的图象与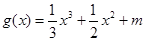 的图象有
的图象有 个不同的交点,求实数
个不同的交点,求实数 的范围.
的范围.
(本小题满分13分)已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A,B的动点,且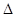 APB面积的最大值为2
APB面积的最大值为2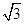 .
.
(1)求椭圆C的方程及离心率;
(2)直线AP与椭圆在点B处的切线交于点D,当直线AP绕点A转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.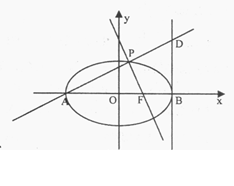
(本小题满分12分)已知各项均为正数的数列 的前
的前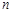 项和为
项和为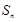 ,且
,且 .在数列
.在数列 中,
中, ,
, .
.
(Ⅰ)求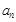 ,
,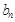 ;
;
(Ⅱ)设 求数列
求数列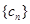 的前项和
的前项和 .
.
(本小题满分12分)为了了解山东省各旅游景点在大众中的熟知度,随机对15~65岁的人群抽样调查了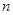 人,回答问题“山东省有哪几个著名的旅游景点?”统计结果如下图表.
人,回答问题“山东省有哪几个著名的旅游景点?”统计结果如下图表.
| 组号 |
分组 |
回答正确的人数 |
回答正确的人数 占本组的频率 |
| 第1组 |
[15,25) |
a |
0.5 |
| 第2组 |
[25,35) |
18 |
x |
| 第3组 |
[35,45) |
b |
0.9 |
| 第4组 |
[45,55) |
9 |
0.36 |
| 第5组 |
[55,65] |
3 |
y |
(1)分别求出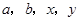 的值;
的值;
(2)从第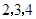 组回答正确的人中用分层抽样的方法抽取6人,求第
组回答正确的人中用分层抽样的方法抽取6人,求第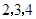 组每组各抽取多少人?
组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.