分别指出下列各组命题构成的“p∧q”“p∨q”“￢p”形式的命题的真假．
（1）p：6＜6．q：6=6；
（2）p：梯形的对角线相等．q：梯形的对角线互相平分；
（3）p：函数y=x2+x+2的图象与x轴没有公共点．q：不等式x2+x+2＜0无解；
（4）p：函数y=cosx是周期函数．q：函数y=cosx是奇函数．
如图，圆O的半径OC垂直于直径AB，弦CD交半径 OA于E，过D的切线与BA的延长线交于M.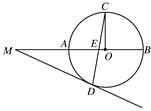
(1)求证：MD＝ME；
(2)设圆O的半径为1，MD＝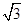
，求MA及CE的长．
如图，已知PE切⊙O于点E，割线PBA交⊙O于A，B两点，∠APE的平分线和AE，BE分别交于点C，D.
求证：(1)CE＝DE；(2)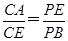
.
如图，AB是⊙O的直径，BE为⊙O的切线，点C为⊙O上不同于A，B的一点，AD为∠BAC的平分线，且分别与BC交于H，与⊙O交于D，与BE交于E，连接BD，CD.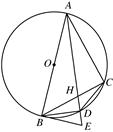
(1)求证：BD平分∠CBE；
(2)求证：AH·BH＝AE·HC.
如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于点D.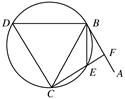
(1)证明：DB＝DC；
(2)设圆的半径为1，BC＝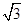
，延长CE交AB于点F，求△BCF外接圆的半径．
如图，D，E分别为△ABC边AB，AC的中点，直线DE交△ABC的外接圆于F，G两点，若CF∥AB，证明：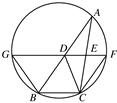
(1)CD＝BC；
(2)△BCD∽△GBD.