某中学将 名高一新生分成水平相同的甲、乙两个“平行班”,每班
名高一新生分成水平相同的甲、乙两个“平行班”,每班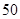 人,吴老师采用
人,吴老师采用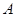 、
、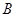 两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取
两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取 名学生的成绩进行统计,作出的茎叶图如下:
名学生的成绩进行统计,作出的茎叶图如下: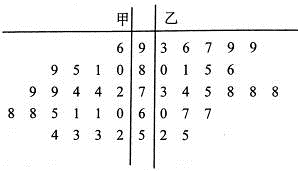
记成绩不低于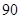 分者为“成绩优秀”.
分者为“成绩优秀”.
(1)在乙班样本的 个个体中,从不低于
个个体中,从不低于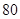 分的成绩中随机抽取
分的成绩中随机抽取 个,记随机变量
个,记随机变量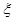 为抽到“成绩优秀”的个数,求
为抽到“成绩优秀”的个数,求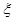 的分布列及数学期望
的分布列及数学期望 ;
;
(2)由以上统计数据填写下面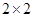 列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?
列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?
甲班(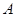 方式) 方式) |
乙班(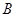 方式) 方式) |
总计 |
|
| 成绩优秀 |
|||
| 成绩不优秀 |
|||
| 总计 |
【改编】设函数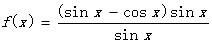 .
.
(1)求 的定义域和最小正周期;
的定义域和最小正周期;
(2)当 ,若
,若
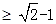 成立,求
成立,求 的取值范围;
的取值范围;
(本小题满分12分)已知函数 ,
,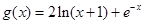 .
.
(Ⅰ) 时,证明:
时,证明: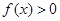 ;
;
(Ⅱ) ,若
,若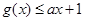 ,求a的取值范围.
,求a的取值范围.
已知抛物线 的焦点为F,点P是抛物线上的一点,且其纵坐标为4,
的焦点为F,点P是抛物线上的一点,且其纵坐标为4, .
.
(1)求抛物线的方程;
(2)设点 ,
, (
( )是抛物线上的两点,∠APB的角平分线与x轴垂直,求△PAB的面积最大时直线AB的方程.
)是抛物线上的两点,∠APB的角平分线与x轴垂直,求△PAB的面积最大时直线AB的方程.
(本小题满分14分)已知各项不为零的数列 的前
的前 项和为
项和为 ,且满足
,且满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设数列 满足
满足 ,求数列
,求数列 的前
的前 项和
项和 .
.