设数列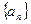 满足
满足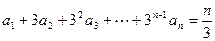
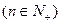
①求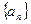 的通项公式;②设
的通项公式;②设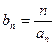 ,求数列
,求数列 的前n项和
的前n项和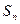 。
。
某水域一艘装载浓硫酸的货船发生侧翻,导致浓硫酸泄漏,对河水造成了污染.为减少对环境的影响,环保部门迅速反应,及时向污染河道投入固体碱,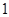 个单位的固体碱在水中逐渐溶化,水中的碱浓度
个单位的固体碱在水中逐渐溶化,水中的碱浓度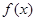 与时间
与时间 (小时)的关系可近似地表示为:
(小时)的关系可近似地表示为: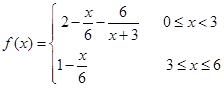 ,只有当污染河道水中碱的浓度不低于
,只有当污染河道水中碱的浓度不低于 时,才能对污染产生有效的抑制作用.
时,才能对污染产生有效的抑制作用.
(Ⅰ) 如果只投放1个单位的固体碱,则能够维持有效的抑制作用的时间有多长?
(Ⅱ) 第一次投放1单位固体碱后,当污染河道水中的碱浓度减少到 时,马上再投放1个单位的固体碱,设第二次投放后水中碱浓度为
时,马上再投放1个单位的固体碱,设第二次投放后水中碱浓度为 ,求
,求 的函数式及水中碱浓度的最大值.(此时水中碱浓度为两次投放的浓度的累加)
的函数式及水中碱浓度的最大值.(此时水中碱浓度为两次投放的浓度的累加)
已知函数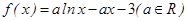 .
.
(I)若a=-1,求函数 的单调区间;
的单调区间;
(Ⅱ)若函数 的图象在点(2,f(2))处的切线的倾斜角为45o,对于任意的t
的图象在点(2,f(2))处的切线的倾斜角为45o,对于任意的t [1,2],函数
[1,2],函数 是
是 的导函数)在区间(t,3)上总不是单调函数,求m的取值范围;
的导函数)在区间(t,3)上总不是单调函数,求m的取值范围;
(Ⅲ)求证:
已知椭圆C的中心在原点,焦点在x轴上,离心率为 ,短轴长为4
,短轴长为4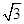 .
.
(I)求椭圆C的标准方程;
(II)直线x=2与椭圆C交于P、Q两点,A、B是椭圆O上位于直线PQ两侧的动点,且直线AB的斜率为 .
.
①求四边形APBQ面积的最大值;
②设直线PA的斜率为 ,直线PB的斜率为
,直线PB的斜率为 ,判断
,判断 +
+ 的值是否为常数,并说明理由.
的值是否为常数,并说明理由.
已知数列{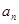 }的前n项和
}的前n项和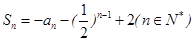 ,数列{
,数列{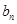 }满足
}满足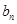 =
=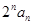 .
.
(I)求证数列{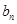 }是等差数列,并求数列{
}是等差数列,并求数列{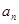 }的通项公式;
}的通项公式;
(Ⅱ)设 ,数列{
,数列{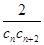 }的前n项和为Tn,求满足
}的前n项和为Tn,求满足 的n的最大值.
的n的最大值.
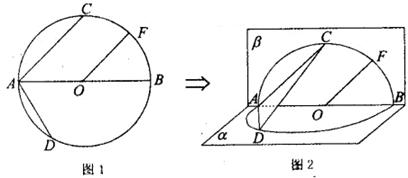
如图1, 的直径AB=4,点C、D为
的直径AB=4,点C、D为 上两点,且
上两点,且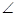 CAB=45°,
CAB=45°,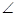 DAB=60°,F为弧BC的中点.沿直径AB折起,使两个半圆所在平面互相垂直,如图2.
DAB=60°,F为弧BC的中点.沿直径AB折起,使两个半圆所在平面互相垂直,如图2.
(I)求证:OF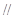 平面ACD;
平面ACD;
(Ⅱ)求二面角C—AD—B的余弦值;
(Ⅲ)在弧BD上是否存在点G,使得FG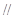 平面ACD?若存在,试指出点G的位置;若不存在,请说明理由.
平面ACD?若存在,试指出点G的位置;若不存在,请说明理由.