如图1, 的直径AB=4,点C、D为
的直径AB=4,点C、D为 上两点,且
上两点,且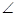 CAB=45°,
CAB=45°,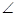 DAB=60°,F为弧BC的中点.沿直径AB折起,使两个半圆所在平面互相垂直,如图2.
DAB=60°,F为弧BC的中点.沿直径AB折起,使两个半圆所在平面互相垂直,如图2.
(I)求证:OF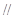 平面ACD;
平面ACD;
(Ⅱ)求二面角C—AD—B的余弦值;
(Ⅲ)在弧BD上是否存在点G,使得FG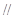 平面ACD?若存在,试指出点G的位置;若不存在,请说明理由.
平面ACD?若存在,试指出点G的位置;若不存在,请说明理由.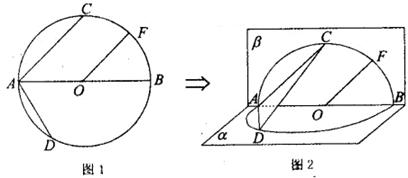
如图所示,已知 M、N分别是AC、AD的中点,BC
M、N分别是AC、AD的中点,BC CD.
CD.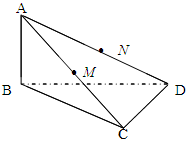
(Ⅰ)求证:MN∥平面BCD;
(Ⅱ)求证:平面B CD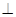 平面ABC;
平面ABC;
(Ⅲ)若AB=1,BC=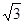 ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角.
(本小题满分10分)
已知函数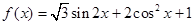
(Ⅰ)求函数 的最小正周期和最小值;
的最小正周期和最小值;
(Ⅱ)设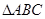 的内角
的内角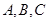 对边分别为
对边分别为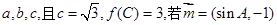 与
与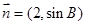 垂直,求
垂直,求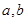 的值.
的值.
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC。
(1)求证:FB=FC;
(2)若AB是△ABC的外接圆的直径,∠EAC =120°,BC=6,求AD的长。
在各项为正的数列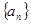 中,数列的前n项和
中,数列的前n项和 满足
满足
(1)求 ;(2) 由(1)猜想数列
;(2) 由(1)猜想数列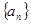 的通项公式;(3) 求
的通项公式;(3) 求
在复平面上,平行四边形ABCD的三个顶点A、B、C 对应的复数分别为 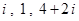 .求第四个顶点D的坐标及此平行四边形的对角线的长.
.求第四个顶点D的坐标及此平行四边形的对角线的长.