已知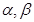 均为锐角,且
均为锐角,且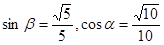 ,求
,求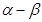 的值。
的值。
某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告费支出为10百万元时,销售额多大?
(可能用到的公式: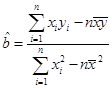 ,
,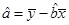 ,其中
,其中 、
、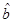 是对回归直线方程
是对回归直线方程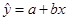 中系数
中系数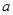 、
、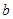 按最小二乘法求得的估计值)
按最小二乘法求得的估计值)
已知函数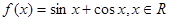
(1)若
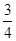 且
且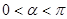 ,求
,求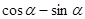 的值
的值
(2)若函数 ,求函数
,求函数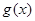 的最大值,并指出取得最大值时相应的
的最大值,并指出取得最大值时相应的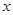 值。
值。
(温馨提示:作答第二小题时请仔细阅读试卷卷首所给的参考公式.)
已知函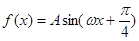 (其中
(其中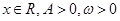 )的最大值为2,最小正周期为8.
)的最大值为2,最小正周期为8.
(1)求函数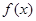 的解析式;
的解析式;
(2)若函数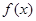 图象上的两点P,Q的横坐标依次为2,4,O坐标原点,求
图象上的两点P,Q的横坐标依次为2,4,O坐标原点,求 的面积.
的面积.
已知函数
(1)利用“五点画图法”:填表并在给出的直角坐标系中画出函数 的一个周期的图象;
的一个周期的图象;
(2)由 的图像经过怎样变换得到
的图像经过怎样变换得到 的图像。
的图像。
列表:
 |
|||||
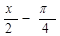 |
|||||
 |

已知函数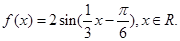
(1)求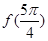 的值;
的值;
(2)求函数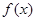 的单调递增区间。
的单调递增区间。