（本题10分）如图1，抛物线y=－x2＋2bx＋c（b＞0）与y轴交于点C，点P为抛物线顶点，分别作点P，C关于原点O的对称点P′，C′，顺次连接四点得四边形PC P′C′．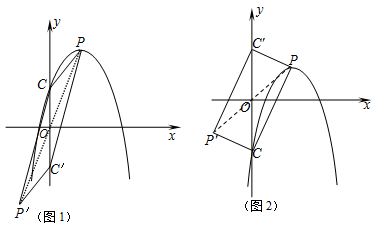
（1）当b=c=1时，求顶点P的坐标；
（2）当b=2，四边形PC P′C′为矩形时（如图2），求c的值；
（3）请你探究：四边形PCP′C′能否成为正方形？若能，求出符合条件的b，c的值；若不能，请说明理由．
已知关于x的一元二次方程x2－（m＋6）x＋3m＋9＝0的两个实数根分别为x1，x2．
（1）求证：该一元二次方程总有两个实数根；
（2）若n＝4（x1＋x2）－x1x2，判断动点P（m，n）所形成的函数图象是否经过点 A（1，16），并说明理由．
如图，一条公路的转弯处是一段圆弧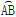
．
（1）作出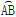所在圆的圆心O；（用直尺和圆规作图，保留作图痕迹，不写作法）
（2）若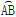的中点C到弦AB的距离为20m，AB＝80m，求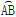所在圆的半径．
已知，△ABC在直角坐标平面内，三个顶点的坐标分别为A（－2， 2）、B（－1，0）、C（0，1）（正方形网格中每个小正方形的边长是一个单位长度）．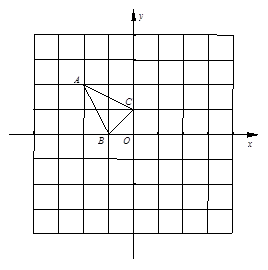
（1）画出△ABC关于y轴的轴对称图形△A1B1C1；
（2）以点O为位似中心，在网格内画出所有符合条件的△A2B2C2，使△A2B2C2与△A1B1C1位似，且位似比为2：1；
（3）求△A1B1C1与△A2B2C2的面积比．
如图，已知点D是△ABC的边AC上的一点，连接BD．∠ABD＝∠C，AB＝6，AD＝4．
（1）求证：△ABD∽△ACB；
（2）求线段CD的长．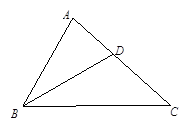
解方程
（1）（x－2）2=9；
（2）3x2－1＝2 x（配方法）；
（3）x2＋3 x＋1＝0；
（4）（x＋1）2－6（x＋1）＋5＝0．