（本题12分）如图，过点A（0，3）的直线l1与x轴交于点B，tan∠ABO=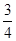
．过点A的另一直线l2：y＝－
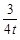x＋b (t＞0)与x轴交于点Q，点P是射线AB上的一个动点，过P作PH⊥x轴于点H，设PB＝5t．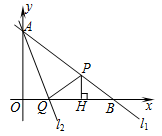
（1）求直线l1 的函数解析式；
（2）当点P在线段AB上运动时，设△PHQ的面积为S（S≠0），求S与t之间的函数关系式（要求写出自变量t的取值范围）；
（3）当点P 在射线AB上运动时，是否存在这样的t值，使以P，H，Q为顶点的三角形与△AOQ相似？若存在，直接写出所有满足条件的t值所对应的P点坐标；若不存在，请说明理由．
、点
在
上，
， 
，
．
．
时，代数式
的值为8，代数式
的值为－14，那么当
时，代数式
的值为多少？
排成2行、2列，两边各加一条竖直线记成
，定义
．若
，求x的值．
，
时，求此时阴影部分的面积．