(本题18分)某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出。当每辆车的月租金每增加50元时,未租出的车将会增加一辆。租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
为了研究化肥对小麦产量的影响,某科学家将一片土地划分成200个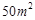 的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)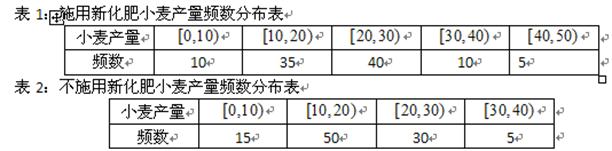
(1)完成下面频率分布直方图;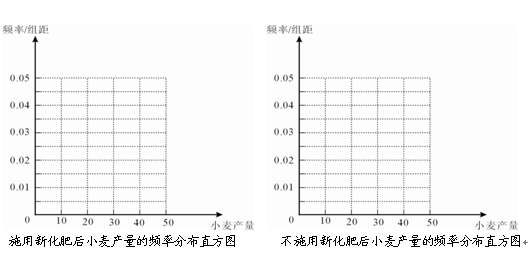
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计施用化肥和不施用化肥的一小块土地的小麦平均产量;
(3)完成下面2×2列联表,并回答能否有99.5%的把握认为“施用新化肥和不施用新化肥的小麦产量有差异”
表3: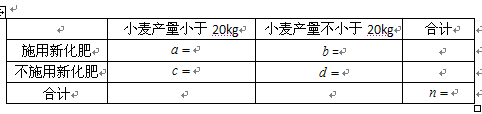
附: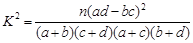
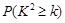 |
0.050 0.010 0.005 0.001 |
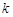 |
3.841 6.635 7.879 10.828 |
把正方形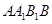 以边
以边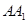 所在直线为轴旋转
所在直线为轴旋转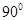 到正方形
到正方形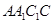 ,其中
,其中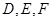 分别为
分别为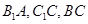 的中点.
的中点.
(1)求证: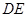 ∥平面
∥平面 ;
;
(2)求证: 平面
平面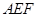 ;
;
(3)求二面角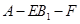 的大小.
的大小.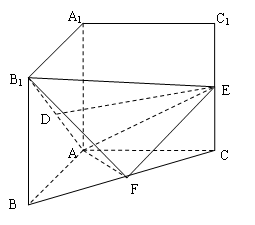
在△ABC中,角A、B、C所对的边分别为a、b、c,已知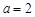 ,
,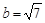 ,
, .
.
(1)求c及△ABC的面积S;
(2)求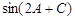
已知函数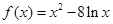 ,
,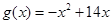 .
.
(Ⅰ)若函数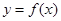 和函数
和函数 在区间
在区间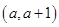 上均为增函数,求实数
上均为增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)若方程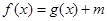 有唯一解,求实数
有唯一解,求实数 的值.
的值.
)已知中心在原点,焦点在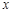 轴上的椭圆
轴上的椭圆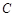 的离心率为
的离心率为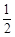 ,且经过点
,且经过点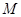
 .
.
(Ⅰ)求椭圆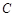 的方程;
的方程;
(Ⅱ)是否存过点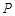 (2,1)的直线
(2,1)的直线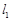 与椭圆
与椭圆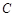 相交于不同的两点
相交于不同的两点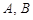 ,满足
,满足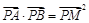 ?若存在,求出直线
?若存在,求出直线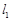 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.