已知关于x的一元二次方程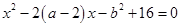 .
.
(1)若a、b是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
(2)若a∈[2,4],b∈[0,6],求方程没有实根的概率.
在锐角 中,内角
中,内角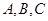 所对的边分别为
所对的边分别为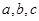 .已知
.已知 .
.
(Ⅰ)求角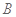 的大小;
的大小;
(Ⅱ)若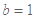 ,求
,求 的面积的最大值.
的面积的最大值.
已知命题 若非
若非 是
是 的充分不必要条件,求
的充分不必要条件,求 的取值范围.
的取值范围.
已知函数
 的图象过坐标原点
的图象过坐标原点 ,且在点
,且在点 处的切线的斜率是
处的切线的斜率是 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求 在区间
在区间 上的最大值;
上的最大值;
(Ⅲ)对任意给定的正实数 ,曲线
,曲线 上是否存在两点
上是否存在两点 ,使得
,使得 是以
是以 为直角顶点的
为直角顶点的
直角三角形,且此三角形斜边中点在 轴上?说明理由.
轴上?说明理由.
已知椭圆 的离心率为
的离心率为 ,短轴端点到焦点的距离为2.
,短轴端点到焦点的距离为2.
(1)求椭圆 的方程;
的方程;
(2)设点 是椭圆
是椭圆 上的任意两点,
上的任意两点, 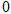 是坐标原点,且
是坐标原点,且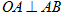 .
.
①求证:原点 到直线
到直线 的距离为定值,并求出该定值;
的距离为定值,并求出该定值;
②任取以椭圆 的长轴为直径的圆上一点
的长轴为直径的圆上一点 ,求
,求 面积的最大值.
面积的最大值.