设向量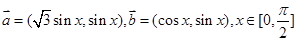 。
。
(Ⅰ)若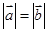 ,求
,求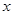 的值;
的值;
(Ⅱ)设函数 ,求
,求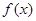 的最大值。
的最大值。
阅读下面材料:
根据两角和与差的正弦公式,有 ------①
------①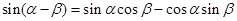 ------②
------②
由①+② 得 ------③
------③
令 有
有
代入③得  .
.
(Ⅰ)类比上述推证方法,根据两角和与差的余弦公式,证明: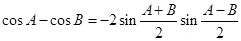 ;
;
(Ⅱ)若 的三个内角
的三个内角 满足
满足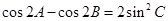 ,试判断
,试判断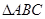 的形状.
的形状.
(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
在直角梯形ABCD中,AD//BC,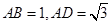 ,
,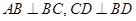 ,如图(1).把
,如图(1).把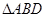 沿
沿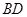 翻折,使得平面
翻折,使得平面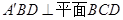 ,如图(2).
,如图(2).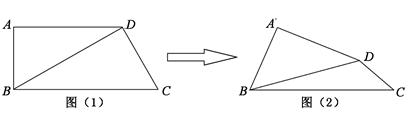
(Ⅰ)求证: ;
;
(Ⅱ)求三棱锥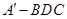 的体积;
的体积;
(Ⅲ)在线段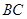 上是否存在点N,使得
上是否存在点N,使得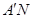
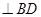 ?若存在,请求出
?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
等差数列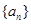 的公差为
的公差为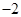 ,且
,且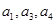 成等比数列.
成等比数列.
(Ⅰ)求数列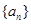 的通项公式;
的通项公式;
(Ⅱ)设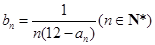 ,求数列
,求数列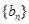 的前
的前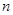 项和
项和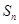 .
.
已知函数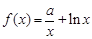 ,
,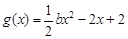 ,
,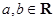
⑴求函数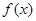 的单调区间;
的单调区间;
⑵记函数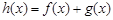 ,当
,当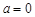 时,
时,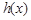 在
在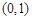 上有且只有一个极值点,求实数
上有且只有一个极值点,求实数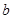 的取值范围;
的取值范围;
⑶记函数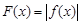 ,证明:存在一条过原点的直线
,证明:存在一条过原点的直线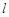 与
与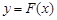 的图象有两个切点
的图象有两个切点
已知椭圆 :
: 的右焦点
的右焦点 在圆
在圆 上,直线
上,直线 交椭圆于
交椭圆于 、
、 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)若 (
(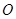 为坐标原点),求
为坐标原点),求 的值;
的值;
(3)设点 关于
关于 轴的对称点为
轴的对称点为 (
( 与
与 不重合),且直线
不重合),且直线
 与
与 轴交于点
轴交于点 ,试问
,试问 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.