德国著名数学家狄利克雷在数学领域成就显著,以其命名的函数f(x)=被称为狄利克雷函数,其中R为实数集,Q为有理数集,则关于函数f(x)有如下四个命题:
①f(f(x))=0;
②函数f(x)是偶函数;
③f(x)是周期函数;
④存在三个点A(x1,f(x1)),B(x2,f(x2)),C(x3,f(x3)),使得△ABC为等边三角形;
⑤存在三个点A(x1,f(x1)),B(x2,f(x2)),C(x3,f(x3)),使得△ABC为直角三角形.
其中真命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
在一次射击比赛中,8个泥制的靶子挂成三列(如图),其中有两列各挂3个,一列挂2个,一位射手按照下列规则去击碎靶子:先挑选一列,然后必须击碎这列中尚未击碎的靶子中最低一个,若每次射击都严格执行这一规则,击碎全部8个靶子的不同方法有
| A.560 | B.320 | C.650 | D.360 |
抛物线y2=2Px,过点A(2,4),F为焦点,定点B的坐标为(8,-8),则|AF|∶|BF|值为
| A.1∶4 | B.1∶2 | C.2∶5 | D.3∶8 |
长方体ABCD-A1B1C1D1中,∠DAD1=45°,∠CAC1=30°那么异面直线AD1与DC1所成角
是
A. |
B.2 |
C.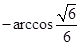 |
D. |
若α、β是两个不同的平面,m、n是两条不同直线,则下列命题不正确的是
| A.α∥β,m⊥α,则m⊥β |
| B.m∥n,m⊥α,则n⊥α |
| C. n∥α,n⊥β,则α⊥β |
D.α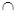 β=m,n与α、β所成的角相等,则m⊥n β=m,n与α、β所成的角相等,则m⊥n |
定义在R上的偶函数f(x)的一个单调递增区间为(3,5),则y=f(x-1)
| A.图象的对称轴为x=-1,且在(2,4)内递增 |
| B.图象的对称轴为x=-1,且在(2,4)内递减 |
| C.图象的对称轴为x=1,且在(4,6)内递增 |
| D.图象的对称轴为x=1,且在(4,6)内递减 |