两质量相同的小球A、B,分别用细线悬挂在等高的O1、O2点,A球的悬线比B球的长,如图所示,把两球均拉到悬线水平后将小球由静止释放,以悬点所在平面为参考平面,则两球经最低点时( )
A.A球的速度大于B球的速度
B.A球的动能等于B球的动能
C.A球的机械能等于B球的机械能
D.A球的机械能小于B球的机械能
如图所示,A、B的质量分别为mA=3kg,mB=2kg,分别固定在轻弹簧两端,盘C的质量mC=1kg,现悬挂于天花板O处,A、B、C均处于静止状态。当烧断O处的细线瞬间,以下说法正确的是(g取10m/s2)( )
A.木块A的加速度aA= 0
B.木块A的加速度aA= 10m/s
C.木块B的加速度aB= 10m/s2
D.木块C的加速度aC= 20m/s2
将一只小球竖直向上抛出,小球运动时受到空气阻力的大小与速度大小成正比,下列描绘小球在上升过程中的加速度大小a及速度大小v与时间t关系的图像,可能正确的是( )
如图所示,A、B是两个摩擦传动轮(不打滑),两轮半径大小关系为RA=2RB,则两轮边缘上的( )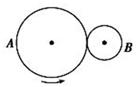
A.角速度之比ωA:ωB=2:1
B.周期之比TA:TB=2:1
C.转速之比nA:nB=2:1
D.向心加速度之比aA:aB=2:1
如图所示,用水平力F推乙物块,使甲、乙、丙三个完全相同的物块沿粗糙水平地面一起做匀加速直线运动,各物块受力的情况是( )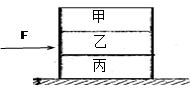
| A.甲物块不受任何摩擦力的作用 |
| B.乙物块只受到一个摩擦力的作用 |
| C.丙物块受到三个摩擦力的作用 |
| D.甲、乙、丙三个物块受到的合力相同 |
一河宽80m,船在静水中的速度为4m/s,水流速度为3m/s,则( )
| A.过河的最小位移是100m,所用时间是20s |
| B.过河的最小位移是80m,所用时间是16s |
| C.过河的最短时间为16s,此时的位移是80m |
| D.过河的最短时间为20s,此时的位移是100m |