（本小题满分12分）如图,
,动点
与
分别在射线
上,且线段
的长为1,线段的长为2,点
分别是线段
的中点.
（Ⅰ）用向量
与
表示向量
;
（Ⅱ）求向量的模.
某百货超市欲在春节期间对某新上市商品开展促销活动，经测算该商品的销售量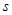
万件与促销费用
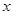万元满足
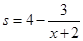．已知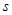万件该商品的进价成本为
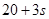万元，商品的销售价格定为
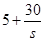元/件．
（1）将该商品的利润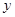
万元表示为促销费用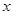万元的函数；
（2）促销费用投入多少万元时，商家的利润最大？最大利润为多少？
已知函数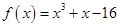
．
（1）求曲线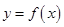
在点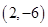
处的切线方程；
（2）直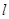线
为曲线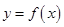的切线，且经过原点，求直线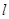的方程及切点坐标．
设函数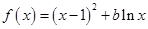
．
（1）若函数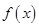
在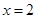
时取得极小值，求
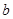的值；
（2）若函数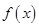在定义域上是单调函数，求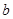的取值范围．
解关于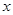
的不等式
．
已知函数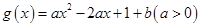
的定义域为[2，3]，值域为[1，4]；设
．
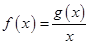（1）求a，b的值；
（2）若不等式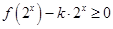
在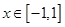
上恒成立，求实数k的取值范围；
（3）若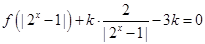
有三个不同的实数解，求实数k的取值范围．