(本小题满分14分) 如图,直角梯形ABCD中,∠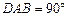 ,AD∥BC,AB=2,AD=
,AD∥BC,AB=2,AD=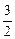 ,BC=
,BC=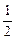 ,椭圆F以A、B为焦点且过点D.
,椭圆F以A、B为焦点且过点D. 
(Ⅰ)建立适当的直角坐标系,求椭圆的方程;


(Ⅱ)若点E满足 ,是否存在斜率
,是否存在斜率

 两点,且
两点,且 ,若存在,求K的取值范围;若不存在,说明理由。
,若存在,求K的取值范围;若不存在,说明理由。
(本小题满分12分) 如图正三棱柱 各条棱长均为1,D是侧棱
各条棱长均为1,D是侧棱 中点。
中点。
(I)求证:平面
(II)求平面
(Ⅲ)求点



(本小题满分12分)


已知在3支不同编号的枪中有2支已经试射校正过,1支未经试射校正。某射手若使用其中校正过的枪,每射击一次击中目标的概率为 ;若使用其中未校正的枪,每射击一次击中目标的概率为
;若使用其中未校正的枪,每射击一次击中目标的概率为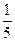 ,假定每次射击是否击中目标相互之间没有影响。
,假定每次射击是否击中目标相互之间没有影响。
(I)若该射手用这2支已经试射校正过的枪各射击一次,求目标被击中的次数为偶数的概率;
(II)若该射手用这3支抢各射击一次,求目标至多被击中一次的概率。
(本小题满分12分)如图所示,在直三棱柱 中,已知
中,已知 ,
, ,
,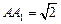 ,
, ,
,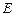 分别为
分别为 、
、 的中点.
的中点.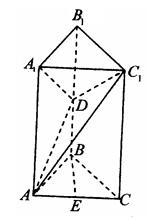
(I)证明: 平面
平面 ;(II)求二面角
;(II)求二面角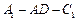 的大小.
的大小.
(本小题满分12分)已知与圆C: 相切的直线
相切的直线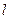 交x轴、y轴于A、B两点,O为坐标原点,且|OA|=
交x轴、y轴于A、B两点,O为坐标原点,且|OA|=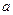 ,
, 。
。
(I)求直线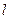 与圆C相切的条件;
与圆C相切的条件;
(II)在(1)的条件下,求线段AB的中点轨迹方程;
(Ⅲ)在(1)的条件下,求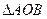 面积的最小值。
面积的最小值。

