抛物线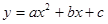 上部分点的横坐标x,纵坐标y的对应值如下表:
上部分点的横坐标x,纵坐标y的对应值如下表:
| x |
… |
-2 |
-1 |
0 |
1 |
2 |
… |
| y |
… |
0 |
-4 |
-4 |
0 |
8 |
… |
(1)根据上表填空:
①抛物线与x轴的交点坐标是 和 ;
②抛物线经过点(-3, );
③在对称轴右侧,y随x增大而 ;
(2)试确定抛物线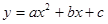 的解析式.
的解析式.
已知方程组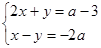 的解都是负数,化简
的解都是负数,化简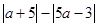 。
。
某实验中学为初二住宿的男学生安排宿舍。如果每间住4人,那么有20人无法安排;如果每间住8人,那么有一间宿舍不空也不满。求宿舍间数和住宿男学生人数。
解方程: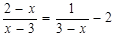
(1)分解因式: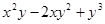
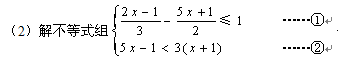 并把解集表示在数轴上。
并把解集表示在数轴上。
(3)计算: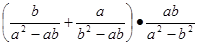
在研究勾股定理时,同学们都见到过图1,∠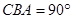 ,四边形
,四边形 、
、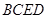 、
、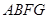 都是正方形.
都是正方形.
⑴连结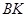 、
、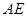 得到图2,则△
得到图2,则△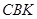 ≌△
≌△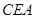 ,此时两个三角形全等的判定依据是
,此时两个三角形全等的判定依据是
▲;过 作
作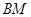 ⊥
⊥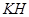 于
于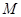 ,交
,交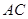 于
于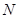 ,则
,则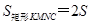 △
△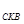 ;同理
;同理 △
△ ,得
,得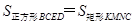 ,然后可证得勾股定理.
,然后可证得勾股定理.
⑵在图1中,若将三个正方形“退化”为正三角形,得到图3,同学们可以探究△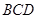 、△
、△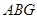 、△
、△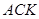 的面积关系是▲.
的面积关系是▲.
⑶为了研究问题的需要,将图1中的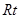 △
△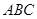 也进行“退化”为锐角△
也进行“退化”为锐角△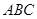 ,并擦去正方形
,并擦去正方形 得图4,由
得图4,由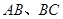 两边向三角形外作正△
两边向三角形外作正△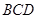 、正△
、正△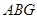 ,△
,△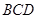 的外接圆与
的外接圆与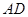 交于点
交于点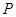 ,此时
,此时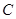 、
、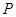 、
、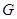 共线,从△
共线,从△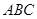 内一点到
内一点到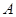 、
、 、
、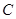 三个顶点的距离之和最小的点恰为点
三个顶点的距离之和最小的点恰为点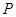 (已经被他人证明).设
(已经被他人证明).设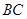 =3,
=3,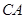 =4,
=4,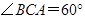 .求
.求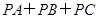 的值.
的值.