在平面直角坐标系xOy中,抛物线 经过点A(0,-2),B(3,4).
经过点A(0,-2),B(3,4).
(1)求抛物线的表达式及对称轴;
(2)设点B关于原点的对称点为C,点D是抛物线对称轴上一动点,记抛物线在A,B之间的部分为图像G(包含A,B两点).若直线CD与图像G有公共点,结合函数图像,求点D纵坐标t 的取值范围.
某校九年级学生共600人,为了解这个年级学生的体能,从中随机抽取部分学生进行1分钟的跳绳测试,并指定甲,乙,丙,丁四名同学对这次测试结果的数据作出整理,下图是这四名同学提供的部分信息: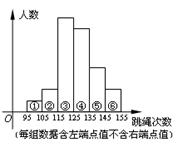
甲:将全体测试数据分成6组绘成直方图(如图).
乙:跳绳次数不少于105次的同学占96%.
丙:第①,②两组频率之和为0.12,且第②组与第⑥组频数都是12.
丁:第②,③,④组的频数之比为4:17:15.
根据这四名同学提供的材料,请解答如下问题:
(1)这次跳绳测试共抽取多少名学生?
(2)如果跳绳次数不少于135次为优秀,根据这次抽查的结果,估计全年级达到跳绳优秀的人数为多少?
写出一个只含字母x的代数式,要求(1)要使此代数式有意义,字母x必须取全体大于1的实数,(2)此代数式的值恒为负数.
为负实数)的均可 |
已知:如图1,平面直角坐标系 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐
标分别为(6,0),(0,2).点D是线段BC上的一个动点(点D与点B,C不重合),过点D作直线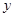 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
(1)在点D运动的过程中,若△ODE的面积为S,求S与 的函数关系式,并写出自变量的取值范围;
的函数关系式,并写出自变量的取值范围;
(2)如图2,当点E在线段OA上时,矩形OABC关于直线DE对称的图形为矩形O′A′B′C′,C′B′分别交CB,OA于点D,M,O′A′分别交CB,OA于点N,E.求证:四边形DMEN是菱形;
(3)问题(2)中的四边形DMEN中,ME的长为____________.

如图,矩形ABCD中,O是AC与BD的交点,过点O的直线EF与AB、C
D的延长线分别交于点E、F.
(1) 求证:△BOE≌△DOF;
(2) 当EF与AC满足什么条件时四边形AECF是菱形,并证明你的结论.
某商店经销一种销售成本为每千克40元的水产品,据市场分析,若按每千克50
元销售,一个月能售出500㎏,销售单价每涨1元,月销售量就减少10㎏,针对这种水产
品,请解答以下问题:
⑴当销售单价定为每千克55元时,计算销售量与月销售利润;
⑵设销售单价为每千克 元,月销售利润为
元,月销售利润为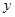 元,求
元,求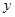 与
与 的关系式;
的关系式;
⑶当销售单价为多少时,月销售利润最大?最大利润是多少?
⑷商店想在销售成本不超过10000元的情况下,使得月销售利润刚好达到8000元,销售单价应为多少?