如图,有一边长为5的正方形ABCD和等腰△PQR,PQ=PR=5cm,QR=8cm,点B,C,Q,R在同一条直线m上,当C,Q两点重合时,等腰△PQR以每秒1cm的速度沿直线m按箭头所示的方向开始匀速运动,t秒后正方形ABCD和等腰△PQR重合部分的面积为Scm2
(1) 当t =3秒时,设PQ与CD相交于点F,点E为QR的中点,连结PE求证:ΔQCF∽ΔQEP
(2)当t =6秒时,求S的值
(3)当8≤t≤13,求S关于t的函数解析式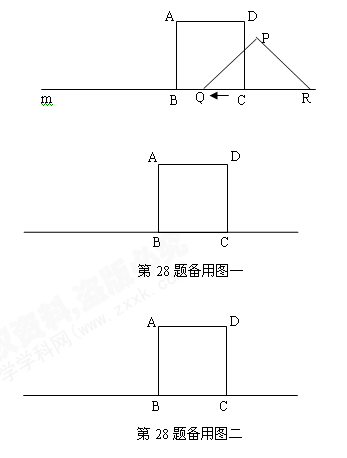
如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
(1)求证:AD=EC;
(2)当∠BAC=Rt∠时,求证:四边形ADCE是菱形.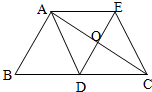
某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系,每盆植入3株时,平均单株盈利3元,以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元,要使每盆的盈利达到10元,每盆应该植多少株?
小明的解法如下:
解:设每盆花苗增加x株,则每盆花苗有(x+3)株,平均单株盈利为(3﹣0.5x)元,
由题意得(x+3)(3﹣0.5x)=10,
化简,整理得:x2﹣3x+=0
解这个方程,得:x1=1,x2=2,
答:要使每盆的盈利达到10元,每盆应该植入4株或5株.
(1)本题涉及的主要数量有每盆花苗株数,平均单株盈利,每盆花苗的盈利等,请写出两个不同的等量关系:_____________________________________________________,
_____________________________________________________________.
(2)请用一种与小明不相同的方法求解上述问题.
研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
| 球的颜色 |
无记号 |
有记号 |
||
| 红色 |
黄色 |
红色 |
黄色 |
|
| 摸到的次数 |
18 |
28 |
2 |
2 |
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
有足够多的长方形和正方形卡片,如下图:
(1)如果选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形的草图,并运用拼图前后面积之间的关系说明这个长方形的代数意义.
这个长方形的代数意义是____________________________
(2)小明想用类似方法解释多项式乘法(a+3b)(2a+b)=2a2+7ab+3b2,那么需用2号卡片 ______张,3号卡片_________张.
解不等式 ,并把解在数轴上表示出来.
,并把解在数轴上表示出来.