(本小题满分12分)经销商经销某种农产品,在一个销售季度内,每售出
 该产品获利润
该产品获利润 元,未售出的产品,每
元,未售出的产品,每
 亏损
亏损 元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了
元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了
 该农产品.以
该农产品.以 (单位:
(单位: ,
, )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量,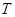 (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(1)将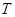 表示为
表示为 的函数;
的函数;
(2)根据直方图估计利润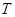 不少于
不少于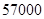 元的概率.
元的概率.
(本小题满分12分)设数列{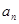 }的前n项和
}的前n项和 满足:
满足: =n
=n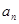 -2n(n-1).等比数列{
-2n(n-1).等比数列{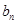 }的前n项和为
}的前n项和为 ,公比为
,公比为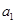 ,且
,且 =
=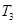 +2
+2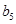 .
.
(1)求数列{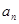 }的通项公式;
}的通项公式;
(2)设数列{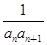 }的前n项和为
}的前n项和为 ,求证:
,求证: ≤
≤ <
<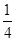 .
.
(本小题满分12分)直三棱柱ABC -A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.
(Ⅰ)求证:AC⊥B1C;
(Ⅱ)若D是AB中点,求证:AC1∥平面B1CD;
(Ⅲ)当
 时,求二面角
时,求二面角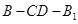 的余弦值.
的余弦值.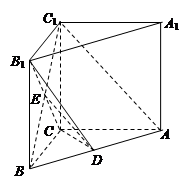
(本小题满分12分)已知向量m ,n
,n ,函数
,函数 m·n. (1)若
m·n. (1)若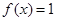 ,求
,求 的值;(2)在锐角△ABC中,角A,B,C的对边分别是
的值;(2)在锐角△ABC中,角A,B,C的对边分别是 ,且满足
,且满足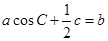 ,求
,求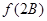 的取值范围.
的取值范围.
(本小题满分14)设函数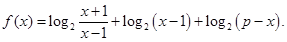
(1)求函数的定义域;
(2)问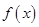 是否存在最大值与
是否存在最大值与 最小值?如果存在,请把它写出来;如果不存在,请说明理由.
最小值?如果存在,请把它写出来;如果不存在,请说明理由.
(本小题满分12分)已知函数f(X)=X+2Xtan -1,X
-1,X 〔-1,
〔-1,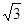 〕其中
〕其中
 (-
(-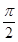 ,
,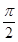 )
)
(1)当 =-
=-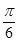 时,求函数的最大值和最小值
时,求函数的最大值和最小值
(2)求 的取值的范围,使Y=f(X)在区间〔-1,
的取值的范围,使Y=f(X)在区间〔-1,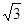 〕上是单调函数
〕上是单调函数