(本小题满分12分)直三棱柱ABC -A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.
(Ⅰ)求证:AC⊥B1C;
(Ⅱ)若D是AB中点,求证:AC1∥平面B1CD;
(Ⅲ)当
 时,求二面角
时,求二面角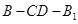 的余弦值.
的余弦值.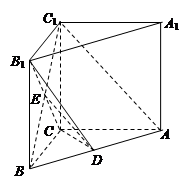
设函数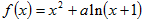 ,其中
,其中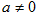 .
.
(Ⅰ)当 时,求曲线
时,求曲线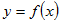 在原点处的切线方程;
在原点处的切线方程;
(Ⅱ)试讨论函数 极值点的个数;
极值点的个数;
(Ⅲ)求证:对任意的 ,不等式
,不等式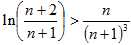 恒成立.
恒成立.
已知椭圆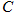 :
: 的离心率为
的离心率为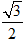 ,右顶点
,右顶点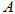 是抛物线
是抛物线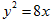 的焦点.直线
的焦点.直线 :
: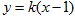 与椭圆
与椭圆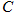 相交于
相交于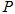 ,
,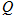 两点.
两点.
(Ⅰ)求椭圆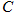 的方程;
的方程;
(Ⅱ)如果 ,点
,点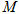 关于直线
关于直线 的对称点
的对称点 在
在 轴上,求
轴上,求 的值.
的值.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF 平面ABCD,EF//AB,
平面ABCD,EF//AB, ,AD=2,AB= AF=2EF=l,点P在棱DF上.
,AD=2,AB= AF=2EF=l,点P在棱DF上.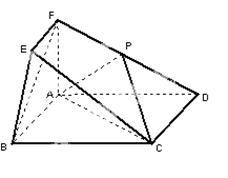
(1)若P为DF的中点,求证:BF//平面ACP
(2)若二面角D-AP-C的余弦值为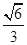 ,求PF的长度.
,求PF的长度.
以下茎叶图记录了甲、乙两名射击运动员训练的成绩(环数),射击次数为4次.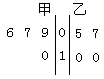
(1)试比较甲、乙两名运动员射击水平的稳定性;
(2)每次都从甲、乙两组数据中随机各选取一个进行比对分析,共选取了4次(有放回选取).设选取的两个数据中甲的数据大于乙的数据的次数为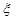 ,求
,求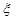 的分布列及数学期望.
的分布列及数学期望.
已知  ,
,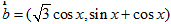 ,记函数
,记函数
(1)求函数 取最大值时
取最大值时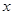 的取值集合;
的取值集合;
(2)设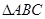 的角
的角 所对的边分别为
所对的边分别为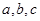 ,若a=2csinA,c=
,若a=2csinA,c= ,且△ABC的面积为
,且△ABC的面积为 ,求a+b的值.
,求a+b的值.