(满分12分)假设关于某设备的使用年限 和所支出的维修费用
和所支出的维修费用 (万元)有如下的统计资料:
(万元)有如下的统计资料:
使用年限 |
 |
 |
 |
 |
 |
维修费用 |
 |
 |
 |
 |
 |
若由资料知 对
对 呈线性相关关系。
呈线性相关关系。
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程 的回归系数
的回归系数 ,
, .
.
(3)估计使用年限为 年时,维修费用是多少?
年时,维修费用是多少? ,
,
(本小题满分16分)
已知数列{an}的前n项和为Sn,且a1=1,Sn=n2an(n∈N*).
(1)试求出S1,S2,S3,S4,并猜想Sn的表达式;
(2)用数学纳法证明你的猜想,并求出an的表达式.
(本小题满分15分)
在5道题中有3道理科题和2道文科题,如果不放回地依次抽取2道题.求:
(1)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第1次抽到理科题的条件下,第2次抽到文科题的概率
(本小题满分15分)
若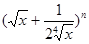
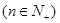 展开式中前三项系数成等差数列.
展开式中前三项系数成等差数列.
(1)求n的值;
(2)求展开式中第4项的系数和二项式系数;
(3)求展开式中x的一次项.
(本小题满分14分)
从5名女同学和4名男同学中选出4人参加四场不同的演讲,分别按下列要求,各有多少种不同选法?
(Ⅰ)男、女同学各2名;
(Ⅱ)男、女同学分别至少有1名;
(Ⅲ)在(Ⅱ)的前提下,男同学甲与女同学乙不能同时选出.
(本小题满分14分)
已知 为复数,
为复数, 和
和 均为实数,其中
均为实数,其中 是虚数单位.
是虚数单位.
(Ⅰ)求复数 ;
;
(Ⅱ)若复数 在复平面上对应的点在第一象限,求实数
在复平面上对应的点在第一象限,求实数 的取值范围.
的取值范围.