（本题共13分）某射击比赛，开始时在距目标
米处射击，如果命中记
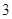分，且停止射击；若第一次射击未命中，可以进行第二次射击，但目标已在
米处，这时命中记
分，且停止射击；若第二次仍未命中还可以进行第三次射击，但此时目标已在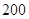
米处，若第三次命中则记
分，并停止射击；若三次都未命中，则记
分．已知射手的命中率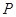
与目标距离
（米）的关系为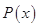
，且在100米处击中目标的概率为
，假设各次射击相互独立．
（Ⅰ）求这名射手在射击比赛中命中目标的概率；
（Ⅱ）求这名射手在比赛中得分
的分布列与数学期望
．
已知数列
是各项均为正数的等差数列，其中
，且
成等比数列；数列
的前
项和为
，满足
.
（1）求数列、的通项公式；
（2）如果
，设数列
的前项和为
，是否存在正整数，使得
成立，若存在，求出的最小值，若不存在，说明理由.
如图所示的多面体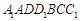
中，底面
为正方形，
//
//
，
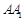，且
．
（Ⅰ）求证：
//
；
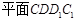（Ⅱ）求多面体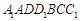的体积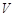
．
已知函数
.
（Ⅰ）当
时，求函数
的最大值；
（Ⅱ）若
，求
的值.
海关对同时从A，B，C三个不同地区进口的某种商品进行抽样检测，从各地区进口此种商品的数量（单位：件）如下表所示. 工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
| 地区 |
A |
B |
C |
| 数量 |
50 |
150 |
100 |
（Ⅰ）求这6件样品中来自A，B，C各地区商品的数量；
（Ⅱ）若在这6件样品中随机抽取2件送往甲机构进行进一步检测，求这2件商品来自相同地区的概率.
（本小题满分13分）已知函数
.
（1）当
时，求
在
处的切线方程；
（2）设函数
，
（ⅰ）若函数
有且仅有一个零点时，求
的值；
（ⅱ）在（ⅰ）的条件下，若
，
，求
的取值范围．