(本小题满分12分)我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.如图,“盾圆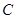 ”是由椭圆
”是由椭圆 与抛物线
与抛物线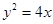 中两段曲线合成,
中两段曲线合成, 为椭圆左、右焦点,
为椭圆左、右焦点, ,
,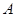 为椭圆与抛物线的一个公共点,
为椭圆与抛物线的一个公共点,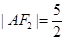 .
.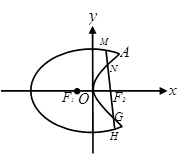
(Ⅰ)求椭圆的方程;
(Ⅱ)是否存在过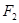 的一条直线
的一条直线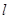 ,与“盾圆
,与“盾圆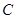 ”依次交于
”依次交于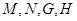 四点,使得
四点,使得 与
与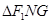 的面积之比为
的面积之比为 ,若存在,求出直线
,若存在,求出直线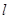 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
设函数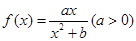
(1)若函数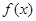 在
在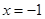 处取得极值-2,求a, b的值.
处取得极值-2,求a, b的值.
(2)若函数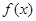 在区间(-1,1)内单调递增,求b的取值范围.
在区间(-1,1)内单调递增,求b的取值范围.
某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下:
| 分组 |
频数 |
频率 |
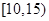 |
10 |
0.25 |
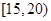 |
24 |
n |
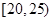 |
m |
P |
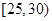 |
2 |
0.05 |
| 合计 |
M |
1 |
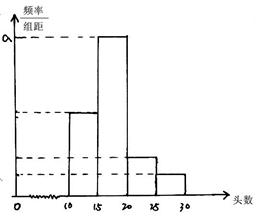
(1)求出表中M,P以及图中a的值.
(2)若该省有这样规模的养殖场240个,试估计该省“瘦肉精”检测呈阳性的猪的头数在区间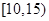 内的养殖场的个数.
内的养殖场的个数.
(3)在所取样本中,出现“瘦肉精”呈阳性猪的头数不少于20头的养殖场中任选2个,求至多一个养殖场出现“瘦肉精”阳性猪头数在区间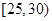 内的概率.
内的概率.
如图,四棱锥P-ABCD的底面是正方形,PD 面ABCD,E是PD上一点.
面ABCD,E是PD上一点.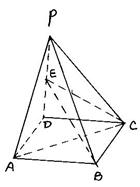
(1)求证:AC BE.
BE.
(2)若PD=AD=1,且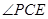 的余弦值为
的余弦值为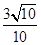 ,求三棱锥E-PBC的体积.
,求三棱锥E-PBC的体积.
已知 ,
,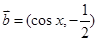 ,若
,若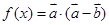 ,求:
,求:
(1)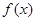 的最小正周期及对称轴方程.
的最小正周期及对称轴方程.
(2)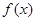 的单调递增区间.
的单调递增区间.
(3)当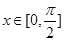 时,函数
时,函数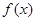 的值域.
的值域.
已知函数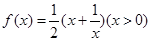 ,
,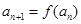 ,对于任意的
,对于任意的 ,都有
,都有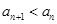 .
.
(1)求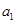 的取值范围
的取值范围
(2)若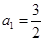 ,证明:
,证明: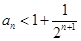 (
(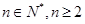 )
)
(3)在(2)的条件下,证明: