已知向量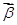 =
= ,变换T的矩阵为A=
,变换T的矩阵为A=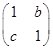 ,平面上的点P(1,1)在变换T作用下得到点P′(3,3),求A-1
,平面上的点P(1,1)在变换T作用下得到点P′(3,3),求A-1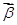 .
.
四棱锥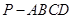 中,侧面
中,侧面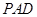 ⊥底面
⊥底面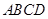 ,底面
,底面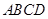 是边长为
是边长为 的正方形,又
的正方形,又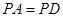 ,
,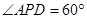 ,
,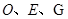 分别是
分别是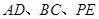 的中点.
的中点.
(Ⅰ)求证: ;
;
(Ⅱ)求二面角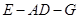 的余弦值.
的余弦值. 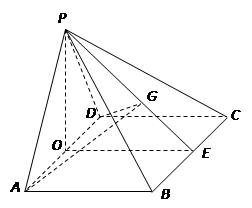
如图,三棱柱 中,侧面
中,侧面
 底面
底面 ,
, ,且
,且 ,O为
,O为 中点.
中点.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面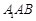 所成角的正弦值
所成角的正弦值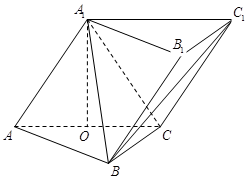
如图所示的长方体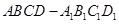 中,底面
中,底面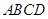 是边长为
是边长为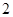 的正方形,
的正方形, 为
为 与
与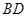 的交点,
的交点, ,
,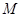 是线段
是线段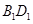 的中点.
的中点.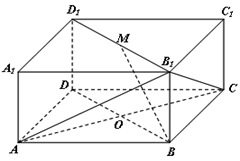
(1)求证: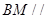 平面
平面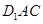 ;
;
(2)求三棱锥 的体积
的体积
把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1∶4,母线长10cm.求:圆锥的母长
(本小题满分12分)
某工厂用7万元钱购买了一台新机器,运输安装费用2千元,每年投保、动力消耗的费用也为2千元,每年的保养、维修、更换易损零件的费用逐年增加,第一年为2千元,第二年为3千元,第三年为4千元,依此类推,即每年增加1千元.问这台机器最佳使用年限是多少年?并求出年平均费用的最小值.(最佳使用年限佳是使年平均费用最小的时间)