数列{ a n}满足a 1＋2 a 2＋22 a 3＋…＋2n－1 a n＝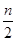
，（n∈N*）前n项和为Sn；数列{bn}是等差数列，且b1=2，其前n项和Tn满足
（
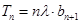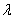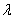为常数，且<1）．
（1）求数列{ a n}的通项公式及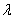的值；
（2）设
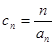，求数列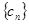
的前n项的和
；
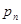（3）证明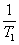
+
+
+ +
>
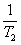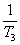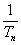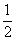Sn．
（本小题满分12分）已知幂函数
的图象经过点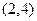
，对于偶函数
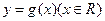，当
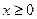时，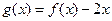
。
（1）求函数的解析式；
（2）求当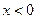
时，函数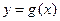
的解析式，并在给定坐标系下，画出函数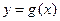的图象
（3）写出函数
的单调递减区间
（本小题满分12分）
已知集合
, 
.
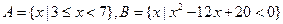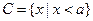（1）求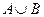
；
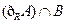
（2）若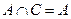
,求
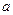的取值范围
（本小题满分14分
函数
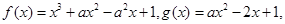实数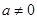
．
（I）若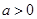
，求函数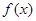
的单调区间；
（II）当函数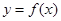
与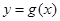
的图象只有一个公共点且
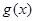存在最小值时，记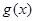的最小值为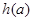
，求的值域；
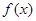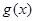（III）若与在区间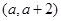
内均为增函数，求
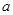的取值范围。
（文）已知函数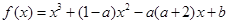
．
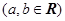（I）若函数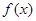的图象过原点，且在原点处的切线斜率是
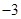，求
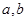的值；
（II）若函数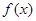在区间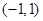
上不单调，求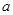的取值范围
（本小题满分12分）
数列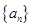
满足
（1）求数列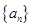的通项公式；
(2)令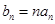
，求数列的前n
项和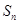
（本小题满分12分）
已知
是等比数列, 
，
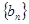是等差数列，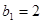
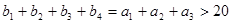
（1）求数列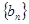的通项公式；
（2）求数列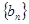的前n项和
；
（3）设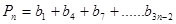
，
其中n=1,2,......,试比较
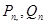的大小。