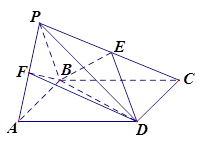
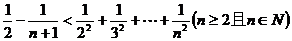（本小题满分13分，（Ⅰ）小问6分，（Ⅱ）小问7分）如图，四棱锥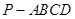
中，
是正三角形，四边形
是矩形，且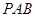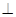平面
平面，
，
．
（Ⅰ）若点
是
的中点，求证：
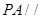平面
；
（Ⅱ）若点
在线段
上，且
，当三棱锥
的体积为
时，求实数
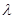的值.
附加题
设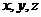
是正实数，且
。
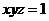证明：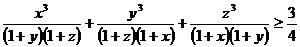
已知函数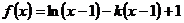
（1）求函数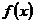
的单调区间和最大值；
（2）若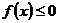
恒成立，求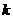
的取值范围；
（3）证明：①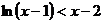
在
上恒成立；
②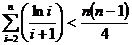
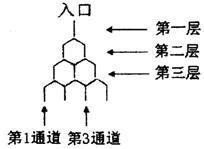
图中竖直线段和斜线段都表示通道，并且在交点处相遇，若竖直线段有一条的为第一层，有两条的为第二层，以此类推，竖直线段有
条的为第层，每一层的竖直通道从左到右分别称为第1通道、第2通道，……，现在有一个小球从入口向下（只能向下，不能向上）运动，小球在每个交点处向左到达下一层或者向右到达下一层的可能性是相同的。小球到达第层第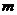
通道的不同路径数称为
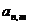，如小球到达第二层第1通道和第二层第2通道的路径都只有一种情况，因此，
，
。
求：（1）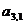
，
，
；
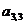（2）
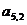，以及小球到达第5层第2通道的概率；
（3）猜想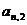
，并证明；
（4）猜想
（不用证明）。
已知函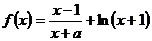数
，其中实数
。
（1）若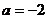
，求曲线
在点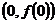
处的切线方程；
（2）若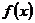
在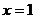
处取得极值，试讨论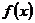的单调性。
求证：