已知函数y=f(x)在R上为奇函数,且当x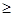 0时,f(x)=
0时,f(x)=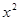 -2x,则f(x)在
-2x,则f(x)在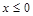 时的解析式是()
时的解析式是()
A. f(x)=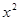 -2x -2x |
B.f(x)=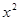 +2x +2x |
C.f(x)= -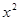 +2x +2x |
D.f(x)= -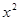 -2x -2x |
函数 在区间
在区间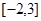 是增函数,则
是增函数,则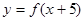 的递增区间是()
的递增区间是()
A.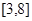 |
B.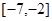 |
C. |
D.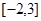 |
为了得到函数 的图像,只需把函数
的图像,只需把函数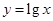 的图像上所有的点()
的图像上所有的点()
| A.向左平移3个单位长度,再向上平移1个单位长度 |
| B.向右平移3个单位长度,再向上平移1个单位长度 |
| C.向左平移3个单位长度,再向下平移1个单位长度 |
| D.向右平移3个单位长度,再向下平移1个单位长度 |
已知函数y=f(x)是定义在R上的奇函数,则下列函数中是奇函数的是()
①y=f(|x|);②y=f(-x);③y=x·f(x);④y=f(x)+x.
| A.①③ | B.②③ | C.①④ | D.②④ |
下列特称命题中,假命题是( ) C
| A.∃x∈R,x2-2x-3=0 | B.至少有一个x∈Z,x能被2和3整除 |
| C.存在两个相交平面垂直于同一直线 | D.∃x∈{x|x是无理数},使x2是有理数 |