(本题10分)已知:等腰三角形的周长为80.
(1)写出底边长y与腰长x的函数表达式;
(2)当腰长为30时,底边长为多少?
(3)当底边长为8时,腰长为多少?
如图,一段河坝的横截面为梯形ABCD,试根据图中数据,求出坝底宽AD.(i=CE:ED,单位:m)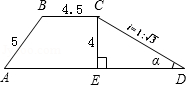
如图,AF=DC,BC∥EF,请只补充一个条件,使得△ABC≌△DEF,并说明理由.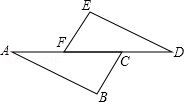
解不等式组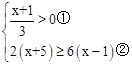 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
已知:如图一,抛物线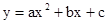 与x轴正半轴交于A、B两点,与y轴交于点C,直线
与x轴正半轴交于A、B两点,与y轴交于点C,直线 经过A、C两点,且AB=2.
经过A、C两点,且AB=2.
(1)求抛物线的解析式;
(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒 ;设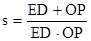 ,当t为何值时,s有最小值,并求出最小值。
,当t为何值时,s有最小值,并求出最小值。
(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由。
.某私营服装厂根据2011年市场分析,决定2012年调整服装制作方案,准备每周(按120工时计算)制作西服、休闲服、衬衣共360件,且衬衣至少60件。已知每件服装的收入和所需工时如下表:
| 服装名称 |
西服 |
休闲服 |
衬衣 |
| 工时/件 |
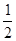 |
 |
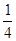 |
| 收入(百元)/件 |
3 |
2 |
1 |
设每周制作西服x件,休闲服y件,衬衣z件。
(1)请你分别从件数和工时数两个方面用含有x,y 的代数式表示衬衣的件数z,
(2)求y与x之间的函数关系式。
(3)问每周制作西服、休闲服、衬衣各多少件时,才能使总收入最高?最高总收入是多少?