如图,在由边长为1的小正方形组成的网格图中有△ABC,建立平面直角坐标系后,点O的坐标是(0,0).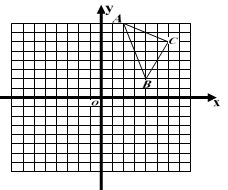
(1)以O为位似中心,作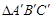 ∽
∽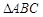 ,相似比为1:2,且保证
,相似比为1:2,且保证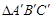 在第三象限;
在第三象限;
(2)点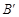 的坐标为( , );
的坐标为( , );
(3)若线段BC上有一点D,它的坐标为(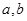 ),那么它的对应点
),那么它的对应点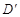 的坐标为( , ).
的坐标为( , ).
作图题:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵黄桷树.如图,要求黄桷树的位置点P到边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种黄桷树的位置点P(不写作法,保留作图痕迹).
(1)如图1,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ABE绕点A逆时针旋转90后,得到△AFC,连接DF.
试说明:①△AED≌△AFD;
② ;
;
(2)如图2,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,D是斜边BC上一点,BD=5,BC=17,求DE的长.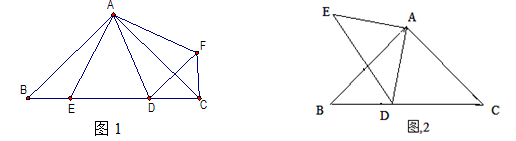
如图,在平面直角坐标系中,OA=OB=OC=8,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的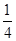 .
.
(1)求点D的坐标;
(2)过点C作CE⊥AD,交AB交于F,垂足为E.求证:OF=OG;
(3)若点F的坐标为(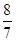 ,0),在第一象限内是否存在点P,使△CFP是以CF为腰长的等腰直角三角形,若存在,请求出点P坐标;若不存在,请说明理由.
,0),在第一象限内是否存在点P,使△CFP是以CF为腰长的等腰直角三角形,若存在,请求出点P坐标;若不存在,请说明理由.
如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.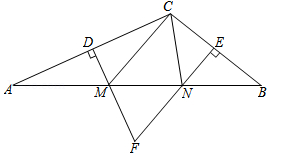
(1)若△CMN的周长为15cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.
如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点.
(1)若EF=4,BC=10,求△EFM的周长;
(2)若∠ABC=50°,∠ACB=70°,求∠MEF的度数.