已知矩阵A=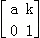 (k≠0)的一个特征向量为
(k≠0)的一个特征向量为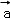 =
=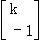 ,矩阵A的逆矩阵A﹣1对应的变换将点(3,1)变为点(1,1).
,矩阵A的逆矩阵A﹣1对应的变换将点(3,1)变为点(1,1).
(1)求实数a,k的值;
(2)求直线x+2y+1=0在矩阵A的对应变换下得到的图形方程.
已知数列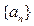 是首项为1的等差数列,其公差
是首项为1的等差数列,其公差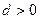 ,且
,且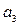 ,
,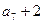 ,
,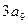 成等比数列.
成等比数列.
(1)求数列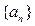 的通项公式;
的通项公式;
(2)设数列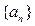 的前n项和为
的前n项和为 ,求
,求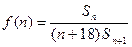 的最大值.
的最大值.
已知函数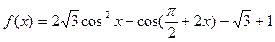
(1)求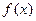 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)若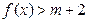 在
在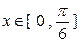 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
已知 为
为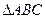 的三个内角,且其对边分别为
的三个内角,且其对边分别为 ,且
,且 .
.
(1)求角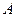 的值;
的值;
|
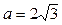 ,
, ,求
,求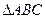 的面积.
的面积.
(本小题满分12分)过椭圆 引两条切线PA、PB、A、B为切点,如直线AB与x轴、y轴交于M、N两点.
引两条切线PA、PB、A、B为切点,如直线AB与x轴、y轴交于M、N两点.
(1)若 ,求P点坐标;
,求P点坐标;
(2)求直线AB的方程(用 表示);
表示);
(3)求△MON面积的最小值.(O为原点)
(本小题满分12分)某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其他两观测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上).