已知矩阵M=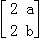 的两个特征值分别为λ1=﹣1和λ2=4.
的两个特征值分别为λ1=﹣1和λ2=4.
(1)求实数a,b的值;
(2)求直线x﹣2y﹣3=0在矩阵M所对应的线性变换作用下的象的方程.
如图几何体上半部分是母线长为5,底面圆半径为3的圆锥,下半部分是下底面圆半径为2,母线长为2的圆台,计算该几何体的表面积和体积。
已知函数 图像上一点
图像上一点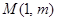 处的切线方程为
处的切线方程为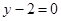 ,其中
,其中 为常数.
为常数.
(Ⅰ)函数 是否存在单调减区间?若存在,则求出单调减区间(用
是否存在单调减区间?若存在,则求出单调减区间(用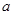 表示);
表示);
(Ⅱ)若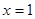 不是函数
不是函数 的极值点,求证:函数
的极值点,求证:函数 的图像关于点
的图像关于点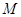 对称.
对称.
(本小题满分14分)
如图,已知椭圆 的离心率
的离心率 ,左、右焦点分别为
,左、右焦点分别为 、
、 ,点
,点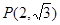 满足:
满足: 在线段
在线段 的中垂线上.
的中垂线上.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若斜率为 的直线
的直线 与
与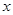 轴、椭圆
轴、椭圆 顺次相交于点
顺次相交于点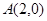 、
、 、
、 ,且
,且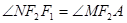 ,求
,求 的取值范围.
的取值范围.
(本小题满分14分)
设Sn表示数列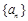 的前n项和.
的前n项和.
(Ⅰ)若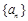 为等差数列,推导Sn的计算公式;
为等差数列,推导Sn的计算公式;
(Ⅱ)若 , 且对所有正整数n, 有
, 且对所有正整数n, 有 .判断
.判断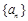 是否为等比数列.
是否为等比数列.
(本小题满分14分)
长方体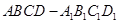 中,
中, ,
,  ,
, 是底面对角线的交点。
是底面对角线的交点。
(Ⅰ)求证: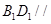 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求三棱锥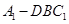 的体积。
的体积。