(本小题满分14分)
如图,已知椭圆 的离心率
的离心率 ,左、右焦点分别为
,左、右焦点分别为 、
、 ,点
,点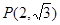 满足:
满足: 在线段
在线段 的中垂线上.
的中垂线上.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若斜率为 的直线
的直线 与
与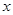 轴、椭圆
轴、椭圆 顺次相交于点
顺次相交于点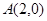 、
、 、
、 ,且
,且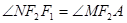 ,求
,求 的取值范围.
的取值范围.
已知函数f(x)=logm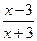
(1)若f(x)的定义域为[α,β],(β>α>0),判断f(x)在定义域上的增减性,并加以说明;
(2)当0<m<1时,使f(x)的值域为[logm[m(β–1)],logm[m(α–1)]]的定义域区间为[α,β](β>α>0)是否存在?请说明理由.
已知a、b为实数,且b>a>e,其中e为自然对数的底,
求证: ab>ba.
设f(x)=ax3+x恰有三个单调区间,试确定a的取值范围,并求其单调区间.
已知f(x)=x2+c,且f[f(x)]=f(x2+1)
(1)设g(x)=f[f(x)],求g(x)的解析式;
(2)设φ(x)=g(x)-λf(x),试问:是否存在实数λ,使φ(x)在(-∞,-1)内为减函数,且在(-1,0)内是增函数.
设关于x的方程2x2-ax-2=0的两根为α、β(α<β),函数f(x)= .
.
(1)求f(α)·f(β)的值;
(2)证明f(x)是[α,β]上的增函数;
(3)当a为何值时,f(x)在区间[α,β]上的最大值与最小值之差最小?