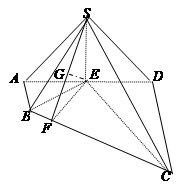已知直线 ,双曲线
,双曲线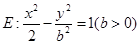 .
.
(1)若直线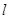 与双曲线E的其中一条渐近线平行,求双曲线E的离心率;
与双曲线E的其中一条渐近线平行,求双曲线E的离心率;
(2)若直线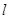 过双曲线的右焦点
过双曲线的右焦点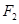 ,与双曲线交于P、Q两点,且
,与双曲线交于P、Q两点,且 ,求双曲线方程.
,求双曲线方程.
选修4-4:坐标系与参数方程
在直角坐标系xOy中,直线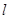 的参数方程为
的参数方程为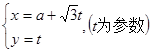 .在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
.在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为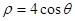 .
.
(Ⅰ)求圆C在直角坐标系中的方程;
(Ⅱ)若圆C与直线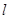 相切,求实数a的值.
相切,求实数a的值.
选修4—1:几何证明选讲
如图,锐角△ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为内切圆I与边CA的切点.
(Ⅰ)求证:四点A,I,H,E共圆;
(Ⅱ)若∠C=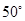 ,求∠IEH的度数.
,求∠IEH的度数.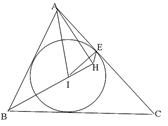
设函数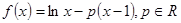 .
.
(Ⅰ)当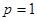 时,求函数
时,求函数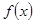 的单调区间;
的单调区间;
(Ⅱ)设函数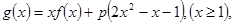 求证:当
求证:当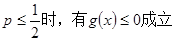
在△ABC中,顶点A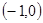 ,B
,B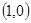 ,动点D,E满足:①
,动点D,E满足:①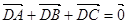 ;②
;②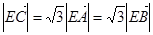 ,③
,③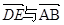 共线.
共线.
(Ⅰ)求△ABC顶点C的轨迹方程;
(Ⅱ)若斜率为1直线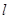 与动点C的轨迹交与M,N两点,且
与动点C的轨迹交与M,N两点,且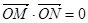 ,求直线
,求直线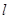 的方程.
的方程.
如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=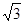 ,SE⊥AD.
,SE⊥AD.
(Ⅰ)证明:平面SBE⊥平面SEC;
(Ⅱ)若SE=1,求三棱锥E-SBC的高.